广东省深圳市罗湖区2017-2018学年九年级上学期数学期末考试试卷
试卷更新日期:2018-02-07 类型:期末考试
一、选择题
-
1. 袋中装有5个白球,3个黑球,除颜色外均相同,从中一次任摸出一个球,则摸到黑球的概率是( )A、 B、 C、 D、2. 一位小朋友拿一个等边三角形木框在阳光下玩,等边三角形木框在地面上的影子不可能是( )A、
 B、
B、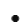 C、
C、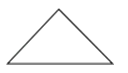 D、
D、 3. 下列图形中,既是轴对称图形又是中心对称图形的有( )
3. 下列图形中,既是轴对称图形又是中心对称图形的有( )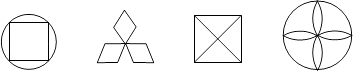 A、4个 B、3个 C、2个 D、1个4. 在Rt△ABC中,∠C=90。 , 若sinA= ,则∠A的度数是( )A、60° B、45° C、30° D、无法确定5. 若关于X的一元二次方程X2一X一3m=0有两个不相等的实数根,则m的取值范围是( )
A、4个 B、3个 C、2个 D、1个4. 在Rt△ABC中,∠C=90。 , 若sinA= ,则∠A的度数是( )A、60° B、45° C、30° D、无法确定5. 若关于X的一元二次方程X2一X一3m=0有两个不相等的实数根,则m的取值范围是( )
A、 m> B、 m< C、 m>一 D、 m<一6. 下列命题中,属于假命题的是( )A、有一个锐角相等的两个直角三角形一定相似 B、对角线相等的菱形是正方形 C、抛物线y=y2-20x+17的开口向上 D、在一次抛掷图钉的试验中,若钉尖朝上的频率为3/5,则钉尖朝上的概率也为3/57. 由下表估算一元二次方程x2+12x=15的一个根的范围,其中正确的是( )X
1.0
1.1
1.2
1.3
X2+12x
13
14.41
15.84
17.29
A、1.0<x<1.1 B、1.1<x<1.2 C、1.2<x<1.3 D、14.41<x<15.848. 如图,位似图形由三角尺与其在灯光照射下的中心投影组成,相似比为l:2,且三角尺一边长为5cm,则投影三角形的对应边长为( )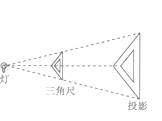
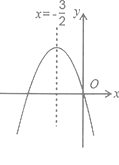
A、8cm B、20cm C、3.2cm D、10cm9. 如图是二次函数y=ax2+bx+c的部分图象,由图象可知,满足不等式ax2+bx+c>0的x的取值范围是( )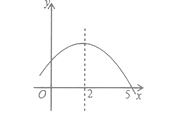 A、-1<x<5 B、x>5 C、x<-1且x>5 D、x<-1或x>510. 如图,已知二次函数y=ax2+bx+c(a#0)的图象如图所示,给出以下四个结论:
A、-1<x<5 B、x>5 C、x<-1且x>5 D、x<-1或x>510. 如图,已知二次函数y=ax2+bx+c(a#0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③b=3a, ④4ac—b2<0;其中正确的结论有( )
 A、1个 B、2个 C、3个 D、4个11. 如图,△AOB是直角三角形,∠AOB=90。 , 0B=2OA,点A在反比例函数 的图象上,点B在反比例函数 的图象上,则k的值是( )
A、1个 B、2个 C、3个 D、4个11. 如图,△AOB是直角三角形,∠AOB=90。 , 0B=2OA,点A在反比例函数 的图象上,点B在反比例函数 的图象上,则k的值是( ) A、-4 B、4 C、-2 D、212. 在边长为3的正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA边上,且满足EB=FC=GD=HA=1,BD分别与HG、HF、EF相交于M、O、N.给出以下结论,
A、-4 B、4 C、-2 D、212. 在边长为3的正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA边上,且满足EB=FC=GD=HA=1,BD分别与HG、HF、EF相交于M、O、N.给出以下结论,①HO=OF ②0F2=ON·OB③HM=2MG ④S△HOM= ,其中正确的个数有( )
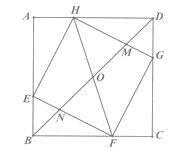 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 有两双完全相同的鞋,从中任取两只,恰好成为一双的概率为 .14. 如图,是一个长方体的主视图、左视图与俯视图(单位:cm),根据图中数据计算这个长方体的体积是cm3 .
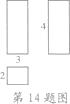 15. 随着数系不断扩大,我们引进新数i,新数i满足交换律,结合律,并规定:i2=-1,那么(2+i)(2-i)=(结果用数字表示).
15. 随着数系不断扩大,我们引进新数i,新数i满足交换律,结合律,并规定:i2=-1,那么(2+i)(2-i)=(结果用数字表示).
16. 如图,Rt△ABC中,∠BAC=90。 , AB=6,sinC= ,以点A为圆心,AB长为半径作弧交AC于M,分别以B、M为圆心,以大于 BM长为半径作弧,两弧相交于N,射线AN与BC相交于D,则AD的长为 .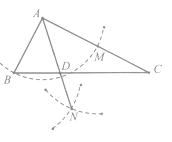
三、解答题
-
17. 解方程:X2-2x-3=018. 小明和小亮玩一个游戏:取三张大小、质地都相同的卡片,上面分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.(1)、请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)、如果和为奇数,则小明胜;若和为偶数,则小亮胜.你认为这个游戏规则对双方公平吗?做出判断,并说明理由.19. 如图,一次函数y=kx+b与反比例函数y= (x>0)的图象相交于A(2,3),B(a,1)两点.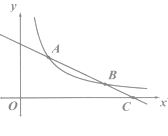 (1)、求这两个函数表达式;
(1)、求这两个函数表达式;
(2)、求证:AB=2BC.
20. 某商场将每件进价为80元的某种商品按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)、若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?(2)、设后来该商品每件降价X元,商场一天可获利润Y元.求出Y与X之间的函数关系式,并求当X取何值时,商场获利润最大?21. 随着科技进步,无人机的应用越来越广,如图,在某一时刻,无人机上的探测器显示,从无人机A处看一栋楼顶部B点的仰角和看与顶部B在同一铅垂线上高楼的底部c的俯角. (1)、如果上述仰角与俯角分别为30。与60。 , 且该楼的高度为30米,求该时刻无人机的竖直高度CD.(2)、如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.22. 如图,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
(1)、如果上述仰角与俯角分别为30。与60。 , 且该楼的高度为30米,求该时刻无人机的竖直高度CD.(2)、如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.22. 如图,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F. (1)、求证:△APD≌△CPD.(2)、当菱形ABCD变为正方形,且PC=2,tan∠PFA= 时,求正方形ABCD的边长.23. 如图,已知抛物线Y=ax2+bx一3与X轴相交于A(一1,0),B(3,0),P为抛物线上第四象限上的点.
(1)、求证:△APD≌△CPD.(2)、当菱形ABCD变为正方形,且PC=2,tan∠PFA= 时,求正方形ABCD的边长.23. 如图,已知抛物线Y=ax2+bx一3与X轴相交于A(一1,0),B(3,0),P为抛物线上第四象限上的点.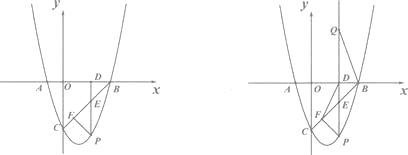 (1)、求该抛物线的函数关系式.(2)、过点P作PD⊥X轴于点D,PD交BC于点E,当线段PE的长度最大时,求点P的坐标.(3)、当线段PE的长度最大时,作PF ⊥BC于点F,连结DF.在射线PD上有一点Q,满足∠PQB=∠DFB,问在坐标轴上是否存在一点R,使得S△RBE=S△QBE;如果存在,直接写出R点的坐标;如果不存在,请说明理由.
(1)、求该抛物线的函数关系式.(2)、过点P作PD⊥X轴于点D,PD交BC于点E,当线段PE的长度最大时,求点P的坐标.(3)、当线段PE的长度最大时,作PF ⊥BC于点F,连结DF.在射线PD上有一点Q,满足∠PQB=∠DFB,问在坐标轴上是否存在一点R,使得S△RBE=S△QBE;如果存在,直接写出R点的坐标;如果不存在,请说明理由.