广东省深圳市罗湖区2017-2018学年七年级上学期数学期末考试试卷
试卷更新日期:2018-02-07 类型:期末考试
一、选择题
-
1. -2的倒数是( )A、 B、-2 C、 D、22. 数据1360000000用科学记数法表示应是( )
A、1.36×10 7 B、1.36×109 C、1.36×1010 D、0.136X 10103. 下列各组数中,互为相反数的是( )A、2与 B、(-1)2与1 C、-1与(-1)2 D、2与4. 下列各式计算正确的是( )A、6a+a2=6a2 B、-2a+5b=3ab C、4m2n-2mn2=2mn D、3ab2-5b2a=-2ab25. 有理数a,b在数轴上的位置如图所示,则a+b是( ) A、正数 B、零 C、负数 D、都有可能6. 对于直线AB,线段CD,射线EF,在下列各图中能相交的是( )A、
A、正数 B、零 C、负数 D、都有可能6. 对于直线AB,线段CD,射线EF,在下列各图中能相交的是( )A、 B、
B、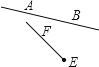 C、
C、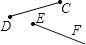 D、
D、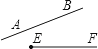 7. 以下调查中,用普查方式收集数据的是( )
7. 以下调查中,用普查方式收集数据的是( )①为了了解全校学生对任课教师的教学意见,学校向全校学生进行问卷调查;
②为了了解初中生上网情况,某市团委对10所初中学校的部分学生进行调查;
③某班学生拟组织一次春游活动,为了确定春游的地点,向全班同学进行调查;
④为了了解全班同学的作业完成情况,对学号为奇数的学生进行调查.
A、①③ B、①② C、②④ D、②③8. 下列变形正确的是( )A、由5=x一2得x=-5-2 B、由5y=0得y= C、由2x=3x+5得-5=3x-2x D、由3x=-2得x=-9. 一收割机收割一块麦田,上午收割了麦田的25%,下午收割了剩下麦田的20%,最后还剩下6公顷麦田未收割.这块麦田一共有( )公顷.A、10 B、12 C、14 D、1610. 某商店有两个进价不同的计算器都卖了80元,其中一个赢利60%,另一个亏本20%,在这次买卖中,这家商店( )A、不赔不赚 B、赚了10元 C、赔了10元 D、赚了50元11. 把弯曲的河道改直,能够缩短航程.这样做的理由是( )
A、两点之间,直线最短 B、两点确定一条直线 C、两点之间,线段最短 D、两点确定一条线段12. 如图所示的正方体展开后的平面图形是( ) A、
A、 B、
B、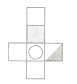 C、
C、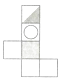 D、
D、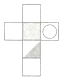
二、填空题
-
13. 比较大小:-2- (用“>”、“<”或“=”填空)14. 若代数式x-y的值为3,则代数式2x-3-2y的值是 .
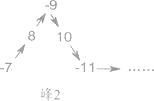
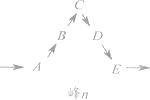
15. 已知线段AB=8cm,在直线AB上画线段BC,使它等于3cm,则线段AC=cm.16. 将一列数-1,2,-3,4,-5,6,……,如图所示有序排列.根据图中排列规律可知,“峰1” 中峰顶位置(C的位置)是4,那么,“峰206”中C的位置的有理数是 .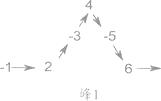
三、解答题
-
17. 计算:(1)、 -17+3;(2)、-32+ ÷(-3).18. 解下列方程:
(1)、4x-7=x+14;(2)、1- =19. 先化简,再求值:5(3a2b-ab2)-( ab2+3a2b),其中a= ,b= .
20. 为了了解某校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况,并将所得数据进行了统计,结果如图所示.
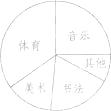 (1)、在这次调查中,一共抽查了多少名学生?
(1)、在这次调查中,一共抽查了多少名学生?
(2)、求出扇形统计图中参加“音乐”活动项目所对应的扇形的圆心角度数;
(3)、若该校有2400名学生,请估计该校参加“美术”活动项目的人数.
21. 下面是小马虎解的一道题.题目:在同一平面上,若∠BOA=70。 , ∠BOC=15。 , 求∠AOC的度数。
解:根据题意画图,如右图所示:
∵∠AOC=∠BOA-∠BOC=70。-15。=55。 ,
∴∠A0C=55。 .

若你是老师,会判小马虎满分吗?若会,请说明理由;若不会,请将小马虎的错误指出,并给出你认为正确的解法.
22. 在艺术节中,甲、乙两校联合准备文艺汇演.甲、乙两校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装(一人买一套)参加演出,下面是服装厂给出的演出服装的价格表:
购买服装的套数
1套至45套
46套至90套
91套以上
每套服装的价格
60
50
40
如果两所学校分别单独购买服装,一共应付5000元.
(1)、如果甲、乙两校联合起来购买服装,那么比各自购买服装节省了多少钱?(2)、甲、乙两校各有多少名学生准备参加演出?(3)、如果甲校有9名同学抽调去参加科技创新比赛不能参加演出,那么你有几种购买方案?通过比较,你该如何购买服装才能最省钱?23. 如图,两个形状、大小完全相同的含有30。角的直角三角板如图1放置,PA、PB与直线MN重合,且三角板PAC和三角板PBD均可以绕点P逆时针旋转.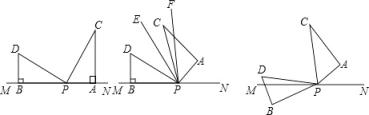 (1)、如图1.则∠DPC为多少度?(2)、如图2,若三角板PAC的边PA从PN处开始绕点P逆时针旋转的角度为α,PF平分∠APD,PE平分∠CPD,求∠EPF的度数;(3)、如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3。/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2。/秒,在两个三角板旋转过程中,当PC转到与PM重合时,两个三角板都停止转动.设两个三角板旋转时间为t秒,请问
(1)、如图1.则∠DPC为多少度?(2)、如图2,若三角板PAC的边PA从PN处开始绕点P逆时针旋转的角度为α,PF平分∠APD,PE平分∠CPD,求∠EPF的度数;(3)、如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3。/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2。/秒,在两个三角板旋转过程中,当PC转到与PM重合时,两个三角板都停止转动.设两个三角板旋转时间为t秒,请问 是定值吗?若是定值,请求出这个定值;若不是定值,请说明理由。
是定值吗?若是定值,请求出这个定值;若不是定值,请说明理由。