广东省深圳市罗湖区2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2018-02-07 类型:期末考试
一、选择题
-
1. 、 、 、(一1)3四个数中最大的数是( )A、 B、 C、 D、(一1)32. 下列运算正确的是( )A、 × = B、 一3=一2 C、 + = D、3 —2 =3. 下列各数:3.14,一 , , , ,其中是无理数的有( )A、4个 B、3个 C、2个 D、1个4. 已知点P关于x轴的对称点P1的坐标是(2,3),那么点P的坐标是( )A、(一2,一3) B、(2,-3) C、(一3,一2) D、(一2,3)5. 汽车以60千米/时的速度在公路上匀速行驶,1小时后进入高速路,继续以100千米/时的速度匀速行驶,则汽车行驶的路程s(千米)与行驶的时间t(时)的函数关系的大致图象是( )A、
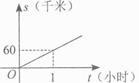 B、
B、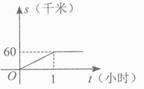 C、
C、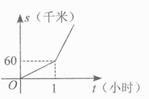 D、
D、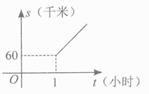 6. 如果数据3,2,x,-3,1的平均数是2,那么x等于( )A、7 B、6 C、5 D、37. 小李家去年节余(节余=收入一支出)5 000元,今年可节余9 500元,并且今年收入比去年高15%,支出比去年低10%,今年的收入与支出各是多少?设去年的收入为X元,支出为Y元,则可列方程组为( )A、 B、 C、 D、8. 如图,a//b,∠1=∠2,∠3=38。 , 则∠4等于( )
6. 如果数据3,2,x,-3,1的平均数是2,那么x等于( )A、7 B、6 C、5 D、37. 小李家去年节余(节余=收入一支出)5 000元,今年可节余9 500元,并且今年收入比去年高15%,支出比去年低10%,今年的收入与支出各是多少?设去年的收入为X元,支出为Y元,则可列方程组为( )A、 B、 C、 D、8. 如图,a//b,∠1=∠2,∠3=38。 , 则∠4等于( )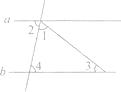 A、38° B、71° C、70° D、61°9. 如果关于x和y的二元一次方程组 的解中的x与y的值相等,那么a的值为( )A、2 B、一2 C、1 D、-110. 若 + = (b为整数),则a的值可以是( )A、 B、27 C、24 D、2011. 下列函数图象不可能是一次函数y=ax一(a一2)图象的是( )A、
A、38° B、71° C、70° D、61°9. 如果关于x和y的二元一次方程组 的解中的x与y的值相等,那么a的值为( )A、2 B、一2 C、1 D、-110. 若 + = (b为整数),则a的值可以是( )A、 B、27 C、24 D、2011. 下列函数图象不可能是一次函数y=ax一(a一2)图象的是( )A、 B、
B、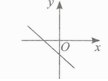 C、
C、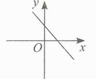 D、
D、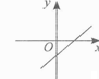 12. 甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的个数有( )
12. 甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的个数有( )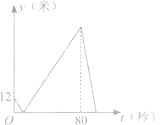
①乙的速度是4米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲从起点到终点共用时83秒;
④乙到达终点时,甲、乙两人相距68米;
⑤乙离开起点12秒后,甲乙第一次相遇.
A、4个 B、3个’ C、2个 D、1个二、填空题
-
13. 16的算术平方根为。14. 一组数据9,2,3,一3,1的极差是 .15. 一次函数y=kx+6的图象与x轴交于点A,与y轴交于点B,S△AOB=9,则k= .
16. 如图所示,在△ABC中, ∠C=2∠B,点D是BC上一点,AD=5,且AD AB,点E是BD上的点,AE= BD,AC=6.5,则AB的长度为 .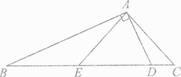
三、解答题
-
17. 解方程组:18. 计算:
(1)、 ;(2)、 ;(3)、19. 某校260名学生参加植树活动,要求每人植树4~7棵,活动结束后随机抽查了20名学生每人的植树数量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的.而条形图尚有一处错误.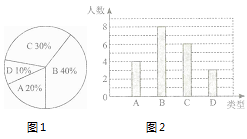
回答下列问题:
(1)、写出条形图中存在的错误,并说明理由;(2)、写出这20名学生每人植树量的众数和中位数;(3)、求这20名学生每人植树量的平均数,并估计这260名学生共植树多少棵.20. 如图,在Rt△ABC中,∠ACB=90。 , AC<BC,D为AB的中点,DE交AC于点E,DF交BC于点F,且DE⊥DF,过点A作AG//BC交FD的延长线于点G. (1)、求证:AG=BF;(2)、若AE=4,BF=8,求线段EF的长.21. 某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.(1)、求每吨水的基础价和调节价;(2)、设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;(3)、若某月用水12吨,应交水费多少元?22. 如图,直线AB:y=一 x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0, ),与直线AB交于点E.
(1)、求证:AG=BF;(2)、若AE=4,BF=8,求线段EF的长.21. 某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.(1)、求每吨水的基础价和调节价;(2)、设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;(3)、若某月用水12吨,应交水费多少元?22. 如图,直线AB:y=一 x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0, ),与直线AB交于点E. (1)、求直线CD的函数关系式;(2)、连接BC,求△BCE的面积;(3)、设点Q的坐标为(m,2),求m的值使得QA+QE值最小.23. 如图1,Rt△ABC中,∠ACB=90。 , 直角边AC在射线OP上,直角顶点C与射线端点0重合,AC=b,BC=a,且满足 .
(1)、求直线CD的函数关系式;(2)、连接BC,求△BCE的面积;(3)、设点Q的坐标为(m,2),求m的值使得QA+QE值最小.23. 如图1,Rt△ABC中,∠ACB=90。 , 直角边AC在射线OP上,直角顶点C与射线端点0重合,AC=b,BC=a,且满足 . (1)、求a,b的值;(2)、如图2,向右匀速移动Rt△ABC,在移动的过程中Rt△ABC的直角边AC在射线OP上匀速向右运动,移动的速度为1个单位/秒,移动的时间为t秒,连接OB,
(1)、求a,b的值;(2)、如图2,向右匀速移动Rt△ABC,在移动的过程中Rt△ABC的直角边AC在射线OP上匀速向右运动,移动的速度为1个单位/秒,移动的时间为t秒,连接OB,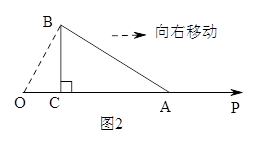
①若△OAB为等腰三角形,求t的值;
②Rt△ABC在移动的过程中,能否使△OAB为直角三角形?若能,求出t的值:若不能,说明理由.