江苏省东台市2018届九年级上学期数学期末考试试卷
试卷更新日期:2018-02-05 类型:期末考试
一、单选题
-
1. 将抛物线y=x2向右平移1个单位长度,再向上平移2个单位长度所得的抛物线解析式为( )A、y=(x﹣1)2+2 B、y=(x+1)2+2 C、y=(x﹣1)2﹣2 D、y=(x+1)2﹣22. 若圆的一条弦把圆分成度数之比为1:3的两条弧,则这条弦所对的圆周角等于( )A、45° B、135° C、90°和270 D、45°和135°3. 下列四个命题:①垂直于弦的直径平分弦以及弦所对的两条弧;②在同圆或等圆中,相等的弦所对的圆周角相等;③三角形有且只有一个外接圆;④矩形一定有一个外接圆;⑤三角形的外心到三角形三边的距离相等。其中真命题的个数有( )A、4个 B、3个 C、2个 D、1个4. 已知二次函数y=ax2﹣bx﹣2(a≠0)的图象的顶点在第四象限,且过点(﹣1,0),当a﹣b为整数时,ab的值为( )
A、 或1 B、 或1 C、 或 D、 或5. 下列方程中,是一元二次方程的是( )A、y= x2﹣3 B、2(x+1)=3 C、x2+3x﹣1=x2+1 D、x2=26. 有15位同学参加智力竞赛,已知他们的得分互不相同,取8位同学进入决赛,小明同学知道了自己的分数后,想知道自己能否进入决赛,还需知道这15位同学的分数的( )A、平均数 B、众数 C、中位数 D、最高分数7. 一个袋中有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,都是蓝色珠子的概率是( )A、 B、 C、 D、8. 已知圆锥的底面半径为6,母线长为8,圆锥的侧面积为( )A、60 B、48 C、60π D、48π二、填空题
-
9. 二次函数 图象的顶点坐标是 .10. 已知实数m是关于x的方程x2-3x-1=0的一根,则代数式m2-3m +5值为 .11. 数据0,1,1,x,3,4的极差是6,则这组数据的x是 .12. 在比例尺为1:38000的扬州旅游地图上,某条道路的长为6cm,则这条道路的实际长度为km.13. AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为 .
 14. 若 、 、 为二次函数 的图象上的三个点,则请你用“<”连接 得 .15. 如图,AB,AC分别是⊙O的直径和弦, 于点D,连结BD、BC, , ,则BD= .
14. 若 、 、 为二次函数 的图象上的三个点,则请你用“<”连接 得 .15. 如图,AB,AC分别是⊙O的直径和弦, 于点D,连结BD、BC, , ,则BD= . 16. 如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,若点M,N分别是AB、BC的中点,则MN长的最大值是 .
16. 如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,若点M,N分别是AB、BC的中点,则MN长的最大值是 . 17. 若二次函数y=ax2+bx+c的图象如图所示,则不等式a(x﹣2)2+b(x﹣2)+c<0的解集为 .
17. 若二次函数y=ax2+bx+c的图象如图所示,则不等式a(x﹣2)2+b(x﹣2)+c<0的解集为 . 18. 如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 .
18. 如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 .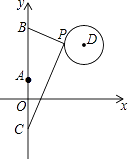
三、解答题
-
19. 计算题:解方程与化简求值
(1)、解方程(2)、已知a:b:c=3:2:5.求 的值.20. 射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):第一次
第二次
第三次
第四次
第五次
第六次
平均成绩
中位数
甲
10
8
9
8
10
9
9
①
乙
10
7
10
10
9
8
②
9.5
(1)、完成表中填空①;②;(2)、请计算甲六次测试成绩的方差;(3)、若乙六次测试成绩方差为 ,你认为推荐谁参加比赛更合适,请说明理由.21. 甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.(1)、若由甲挑一名选手打第一场比赛,选中乙的概率是多少?(直接写出答案)(2)、任选两名同学打第一场,请用树状图或列表法求恰好选中甲、乙两位同学的概率。22. 已知 、 是关于 的方程 的两个不相等的实数根.
(1)、求实数 的取值范围;(2)、已知等腰 的一边长为7,若 、 恰好是 另外两边长,求这个三角形的周长.
23. 已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)、AD=BD;(2)、DF是⊙O的切线.24. 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作: (1)、请在图中确定该圆弧所在圆心D点的位置,求出D点坐标(2)、连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;(3)、若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.25. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且经A(1,0)、B(0,﹣3)两点.
(1)、请在图中确定该圆弧所在圆心D点的位置,求出D点坐标(2)、连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;(3)、若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.25. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且经A(1,0)、B(0,﹣3)两点. (1)、求抛物线的解析式;(2)、在抛物线的对称轴x=﹣1上,是否存在点M,使它到点A的距离与到点B的距离之和最小,如果存在求出点M的坐标,如果不存在请说明理由.26. 某商场销售一种成本为每件30元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=-10x+600,商场销售该商品每月获得利润为w(元).
(1)、求抛物线的解析式;(2)、在抛物线的对称轴x=﹣1上,是否存在点M,使它到点A的距离与到点B的距离之和最小,如果存在求出点M的坐标,如果不存在请说明理由.26. 某商场销售一种成本为每件30元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=-10x+600,商场销售该商品每月获得利润为w(元).
(1)、求w与x之间的函数关系式;(2)、如果商场销售该商品每月想要获得2000元的利润,那么每月成本至少多少元?(3)、为了保护环境,政府部门要求用更加环保的新产品替代该商品,商场销售新产品,每月的销量与销售价格之间的关系与原产品的销售情况相同,新产品的成本每件32元,若新产品每月的销售量不低于200件时,政府部门给予每件4元的补贴,试求定价多少元时,每月销售新产品的利润最大?求出最大的利润。
27. 定义:如果一个数的平方等于 ,记为 ,这个数 叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为 ( 为实数), 叫这个复数的实部, 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:
(1)、填空: = , = .(2)、填空:① ; ② .(3)、若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, ,( 为实数),求 的值.(4)、试一试:请利用以前学习的有关知识将 化简成 的形式.
(5)、解方程:x2 - 2x +4 = 0
28. 如图,抛物线 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC. (1)、求抛物线的解析式;(2)、抛物线上是否存在点M,使得△CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由;(3)、将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、抛物线上是否存在点M,使得△CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由;(3)、将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由.