河南省新乡七中2018届九年级上学期数学期末考试试卷
试卷更新日期：2018-02-05 类型：期末考试
一、单选题
-
1. 若一元二次方程 的常数项是0，则m等于（ ）
A、-3 B、3 C、±3 D、92. 下列所给图形既是中心对称图形，又是轴对称图形的是（ ）
A、正三角形 B、角 C、正方形 D、正五边形3. 一个袋子中装有3个红球和2个黄球，这些球的形状、大小、质地完全相同，在看不到球的条件下，随机从袋中摸出2个球，其中2个球颜色不相同的概率是（ ）A、 B、 C、 D、4. 用配方法解方程 ，配方后可得（ ）
A、 B、 C、 D、5. 如图，⊙O是△ABC的外接圆，∠OCB=40°，则∠A的大小为（ ）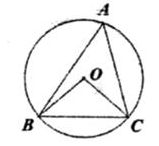
A、40° B、50° C、80° D、100°6. 将抛物线y=﹣3x2平移，得到抛物线y=﹣3 （x﹣1）2﹣2，下列平移方式中，正确的是（ ）
A、先向左平移1个单位，再向上平移2个单位 B、先向左平移1个单位，再向下平移2个单位 C、先向右平移1个单位，再向上平移2个单位 D、先向右平移1个单位，再向下平移2个单位7. 如图，PA、PB是⊙O的两条切线，切点分别是A、B，如果OP=4，PA=2 ，那么 等于（ ）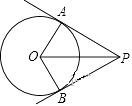
A、90° B、100° C、60° D、110°8. 独山县开展关于精准扶贫、精准扶贫的决策部署以来，某贫困户2014年人均纯收入为2620元，经过帮扶到2016年人均纯收入为3850元，设该贫困户每年纯收入的平均增长率为x，则下面列出的方程中正确的是（ ）
A、2620（1+x）2=3850 B、2620（1+x）=3850 C、2620（1+2x）=3850 D、2620（1+2x）2=38509. 如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．
下面有三个推断：
①当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；
②随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；
③若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的概率一定是0.620．
其中合理的是（ ）
A、① B、② C、①② D、①③10. 如图是二次函数 图象的一部分，对称轴为 ，且经过点（2，0）下列说法：①abc<0；②-2b+c=0；③4a+2b+c<0；④若(- ，y1)，( ，y2)是抛物线上的两点，则y1<y2；⑤ >m(am+b)其中(m≠ )其中说法正确的是（ ）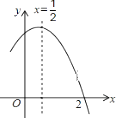
A、①②④⑤ B、③④ C、①③ D、①②⑤二、填空题
-
11. 若关于x的方程x2-mx+m=0有两个相等实数根，则代数式2m2-8m+1的值为。
12. 抛物线y=-x2+2x+2的顶点坐标是 ．
13. 第一盒乒乓球中有4个白球2个黄球，第二盒乒乓球中有3个白球3个黄球，分别从每个盒子中随机地取出1个球，则取出的两个球都是黄球的概率是 ．14. 如图，在△ABC中，∠C=90°，AC=BC= ，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B，则C′B=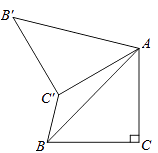
15. 如图，C为半圆内一点，O为圆心，直径AB长为2cm，∠BOC=60°，∠BCO=90°，将△BOC绕圆心O逆时针旋转至△B′OC′，点C′在OA上，则边BC扫过区域（图中阴影部分）的面积为cm2 ．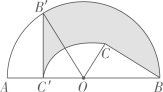
三、解答题
-
16. 解下列方程．
(1)、(x+3)2=2(x+3)(2)、3x(x-1)=2-2x
17. 如图，在平面直角坐标系网格中，△ABC的顶点都在格点上，点C坐标(0，-1)．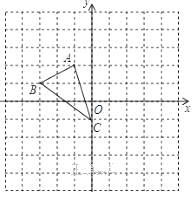
(1)、①作出△ABC 关于原点对称的△A1B1C1 ， 并写出点A1的坐标；②把△ABC 绕点C逆时针旋转90°，得△A2B2C2 ， 画出△A2B2C2 ， 并写出点A2的坐标；
(2)、直接写出△A2B2C2的面积
18. 在一个口袋中有4个完全相同的小球，把它们分别标号为1、2、3、4，随机摸取一个小球然后放回，再随机地摸取一个小球．
(1)、采用树状图法（或列表法）列出两次摸取小球出现的所有可能结果，并回答摸取两球出现的所以可能结果共有几种；
(2)、求两次摸取的小球标号相同的概率；(3)、求两次摸取的小球标号的和等于4的概率；
(4)、求两次摸取的小球标号的和是2的倍数或3的倍数的概率．
19. 已知：如图，AB是⊙O的直径，BC是弦，∠B=30°，延长BA到D，使∠BDC=30°．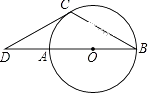
(1)、求证：DC是⊙O的切线；(2)、若AB=2，求DC的长．20. 如图，已知AB是半圆O的直径，点P是半圆上一点，连结BP，并延长BP到点C，使PC=PB，连结AC．
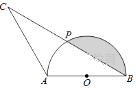(1)、求证：AB=AC.(2)、若AB=4，∠ABC=30°，①求弦BP的长；②求阴影部分的面积．
21. 某超市销售一种牛奶，进价为每箱24元，规定售价不低于进价现在的售价为每箱36元，每月可销售60箱市场调查发现：若这种牛奶的售价每降价1元，则每月的销量将增加10箱，设每箱牛奶降价x元(x为正整数)，每月的销量为y箱．
(1)、写出y与x之间的函数关系式和自变量x的取值范围；(2)、市如何定价，才能使每月销售牛奶的利润最大？最大利润是多少元？22. 如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG、DE．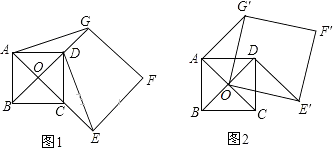
n(1)、求证：DE⊥AG；(2)、正方形ABCD固定，将正方形OEFG绕点O逆时针旋转角(0°< <360°)得到正方形OE’F’G’，如图2．①在旋转过程中，当∠OAG’是直角时，求 的度数；
②若正方形ABCD的边长为1，在旋转过程中，求AF’长的最大值和此时 的度数，直接写出结果不必说明理由．
23. 如图，在平面直角坐标系中，二次函数y=-x2+bx+c的图象与x轴交于A、B两点，与y轴交于C（0，3），A点在原点的左侧，B点的坐标为（3，0）．点P是抛物线上一个动点，且在直线BC的上方．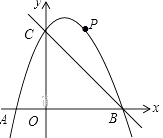
(1)、求这个二次函数的表达式．(2)、连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
(3)、当点P运动到什么位置时，四边形 ABPC的面积最大，并求出此时点P的坐标和四边形面积的最大值。