广东省汕头市潮南区两英镇2018届九年级上学期数学期末考试试卷
试卷更新日期:2018-02-05 类型:期末考试
一、单选题
-
1. 下列方程是一元二次方程的是( )
A、ax2+bx+c=0 B、3x2﹣2x=3(x2﹣2) C、x3﹣2x﹣4=0 D、(x﹣1)2﹣1=02. 已知⊙O的直径为5,若PO=5,则点P与⊙O的位置关系是( )
A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、无法判断3. 二次函数y=x2+2的顶点坐标是( )
A、(1,﹣2) B、(1,2) C、(0,﹣2) D、(0,2)4. 如图,BD是⊙O的直径,点A,C在⊙O上, ,∠AOB=60°,则∠BDC的度数是( )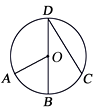 A、60° B、45° C、35° D、30°5. 若x2+4x﹣4=0,则3(x﹣2)2﹣6(x+1)(x﹣1)的值为( )
A、60° B、45° C、35° D、30°5. 若x2+4x﹣4=0,则3(x﹣2)2﹣6(x+1)(x﹣1)的值为( )
A、﹣6 B、6 C、18 D、306. 正十二边形的每一个内角的度数为( )
A、120° B、135° C、150° D、1080°7. 已知点A(1,a)、点B(b,2)关于原点对称,则a+b的值为( )
A、﹣3 B、3 C、﹣1 D、18.在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,则油的最大深度为( )
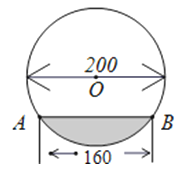 A、40cm B、60cm C、80cm D、100cm9. 如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为( )
A、40cm B、60cm C、80cm D、100cm9. 如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为( )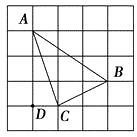 A、10π B、 C、 π D、π10.
A、10π B、 C、 π D、π10.如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
 A、
A、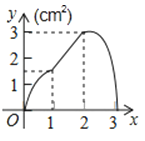 B、
B、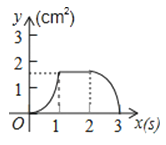 C、
C、 D、
D、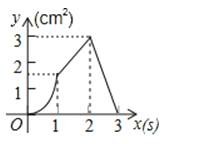
二、填空题
-
11. 一元二次方程x(x+3)=0的解是 .12. 将二次函数 的图象沿x轴向左平移2个单位,则平移后的抛物线对应的二次函数的表达式为 .13. 若|b-1|+ =0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 .
14. 如图,已知等边△ABC的边长为6,以AB为直径的⊙O与边AC、BC分别交于D、E两点,则劣弧 的长为 .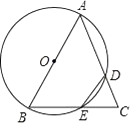 15. 如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是。
15. 如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是。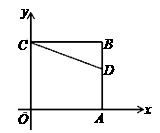 16. 如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,则∠B+∠E= .
16. 如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,则∠B+∠E= .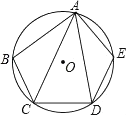
三、解答题
-
17. 用公式法解方程:x2﹣x﹣2=0.
18. 如图为桥洞的形状,其正视图是由 和矩形ABCD构成.O点为 所在⊙O的圆心,点O又恰好在AB为水面处.若桥洞跨度CD为8米,拱高(OE⊥弦CD于点F )EF为2米.求 所在⊙O的半径DO.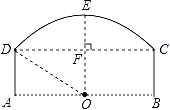 19. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2),将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1 , 并写出A1 , B1的坐标.
19. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2),将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1 , 并写出A1 , B1的坐标.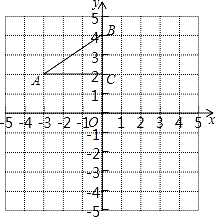 20. 某校九年级举行毕业典礼,需要从九年级(1)班的2名男生、1名女生(男生用A,B表示,女生用a表示)和九年级(2)班的1名男生、1名女生(男生用C表示,女生用b表示)共5人中随机选出2名主持人,用树状图或列表法求出2名主持人来自不同班级的概率.21. 已知抛物线y=ax2+bx﹣8(a≠0)的对称轴是直线x=1,
20. 某校九年级举行毕业典礼,需要从九年级(1)班的2名男生、1名女生(男生用A,B表示,女生用a表示)和九年级(2)班的1名男生、1名女生(男生用C表示,女生用b表示)共5人中随机选出2名主持人,用树状图或列表法求出2名主持人来自不同班级的概率.21. 已知抛物线y=ax2+bx﹣8(a≠0)的对称轴是直线x=1,
(1)、求证:2a+b=0;(2)、若关于x的方程ax2+bx﹣8=0,有一个根为4,求方程的另一个根.
22. 如图1,若△ABC和△ADE为等边三角形,M,N分别是BE,CD的中点,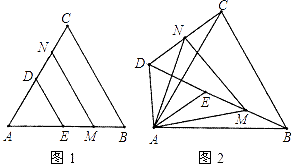 (1)、求证:△AMN是等边三角形.
(1)、求证:△AMN是等边三角形.
(2)、当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由.
23. 用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②中的一种).设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)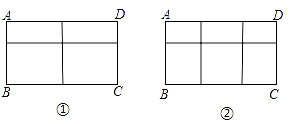 (1)、在图①中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积为3平方米?
(1)、在图①中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积为3平方米?
(2)、在图②中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
24. 如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.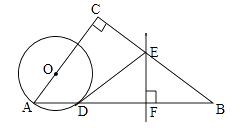 (1)、判断直线DE与⊙O的位置关系,并说明理由;
(1)、判断直线DE与⊙O的位置关系,并说明理由;
(2)、若AC=6,BC=8,OA=2,求线段DE的长.25. 若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.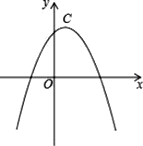 (1)、求抛物线C2的解析式.(2)、点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.(3)、设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.
(1)、求抛物线C2的解析式.(2)、点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.(3)、设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.