甘肃省定西市安定区2018届九年级上学期数学期末考试试卷
试卷更新日期:2018-02-05 类型:期末考试
一、单选题
-
1. 下列图形中不是中心对称图形的是( )
A、等边三角形 B、矩形 C、菱形 D、圆2. 一元二次方程(x+1)2+2016=0的根的情况是( )
A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、无实数根3. 已知反比例函数y=- ,当x>0时,它的图象在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 已知正六边形的边长为2,则它的内切圆的半径为( )
A、1 B、 C、2 D、25. 抛物线y=x2-8x-1的对称轴为( )
A、直线x=4 B、直线x=-4 C、直线x=8 D、直线x=-86. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 B、在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” C、抛一个质地均匀的正六面体骰子,向上的面点数是5 D、抛一枚硬币,出现反面的概率7. 将抛物线y=x2-4x-4向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )A、y=(x+1)2-13 B、y=(x-5)2-3 C、y=(x-5)2-13 D、y=(x+1)2-38. 如图,已知点A在反比例函数y= 的图像上,点B在x轴的正半轴上,且△OAB是面积为 的等边三角形,那么这个反比例函数的解析式是( )
A、 B、 C、 D、9. 如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )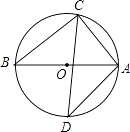 A、20° B、40° C、50° D、70°10. 如图,正方形纸片ABCD的边长为2,翻折∠B,∠D,使两个直角的顶点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设BE=x(0<x<2),阴影部分面积为y,则y与x之间的函数图象为( )
A、20° B、40° C、50° D、70°10. 如图,正方形纸片ABCD的边长为2,翻折∠B,∠D,使两个直角的顶点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设BE=x(0<x<2),阴影部分面积为y,则y与x之间的函数图象为( )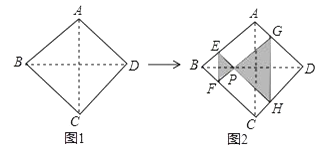 A、
A、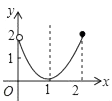 B、
B、 C、3
C、3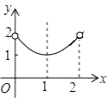 D、
D、
二、填空题
-
11. 若x2﹣4x+5=(x﹣2)2+m,则m= .
12. 若二次函数y=-x2-4x+k的最大值是9,则k= .
13. 如图,某单位准备将院内一块长30m,宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图,要使种植花草的面积为532m2 , 设小道进出口的宽度为x m,根据条件,可列出方程: . 14. 已知y与x-3成正比例,当x=4时,y=-1;那么当x=-4时,y= .15. 如图所示,小明坐在秋千上,秋千旋转了80°,∠AOE=60°,则∠DOB= .
14. 已知y与x-3成正比例,当x=4时,y=-1;那么当x=-4时,y= .15. 如图所示,小明坐在秋千上,秋千旋转了80°,∠AOE=60°,则∠DOB= .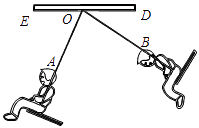 16. 如图,将长为8 cm的铁丝AB首尾相接围成半径为2 cm的扇形,则S扇形=cm2 .
16. 如图,将长为8 cm的铁丝AB首尾相接围成半径为2 cm的扇形,则S扇形=cm2 .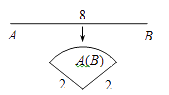 17. 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=1,有以下四个结论:
17. 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=1,有以下四个结论:①abc>0;②b2-4ac>0;③b=-2a;④a+b+c>2.其中正确的是 (填写序号)
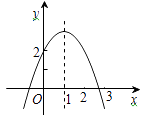 18. 小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是 .
18. 小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是 .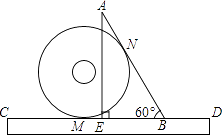
三、解答题
-
19. 解方程:
(1)、x2+3=3(x+3)(2)、4x(2x-1)=3(2x-1)20. 如图,已知⊙O,用尺规作⊙O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑) 21. 某城市体育中考项目分为必测项目和选测项目,必测项目为:跳绳、立定跳远;选测项目为50米、实心球、踢毽子三项中任选一项.
21. 某城市体育中考项目分为必测项目和选测项目,必测项目为:跳绳、立定跳远;选测项目为50米、实心球、踢毽子三项中任选一项.
(1)、每位考生将有种选择方案;(2)、用画树状图或列表的方法求小颖和小华将选择同种方案的概率.22. 已知二次函数当x=-1时,有最小值-4,且当x=0时,y=-3,求二次函数的表达式.
23. 如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y= 图象上. (1)、求m,k的值;(2)、设直线AB与x轴交于点C,求△AOC的面积.24. 如图,点A、B、C、D、E在圆上,弦的延长线与弦的延长线相交于点,AB是圆的直径,D是BC的中点.求证:AB=AC.
(1)、求m,k的值;(2)、设直线AB与x轴交于点C,求△AOC的面积.24. 如图,点A、B、C、D、E在圆上,弦的延长线与弦的延长线相交于点,AB是圆的直径,D是BC的中点.求证:AB=AC.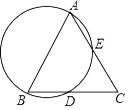 25. 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
25. 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离. 26. 如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高为2.44m.
26. 如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高为2.44m.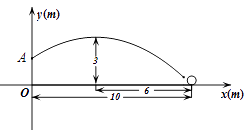 (1)、在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)(2)、守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?27. 如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)、在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)(2)、守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?27. 如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.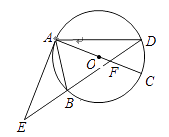 (1)、求证:EA是⊙O的切线;
(1)、求证:EA是⊙O的切线;
(2)、已知点B是EF的中点,AF=4,CF=2,求AE的长.28. 如图,抛物线y=-x 2+bx+c与x轴交于A、B两点,与y轴交于点C,已知经过B、C两点的直线的表达式为y=-x+3.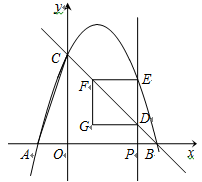
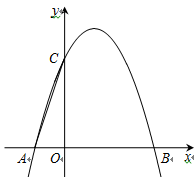 (1)、求抛物线的函数表达式;(2)、点P(m,0)是线段OB上的一个动点,过点P作y轴的平行线,交直线BC于D,交抛物线于E,EF∥x轴,交直线BC于F,DG∥x轴,FG∥y轴,DG与FG交于点G.设四边形DEFG的面积为S,当m为何值时S最大,最大值是多少?(3)、在坐标平面内是否存在点Q,将△OAC绕点Q逆时针旋转90°,使得旋转后的三角形恰好有两个顶点落在抛物线上.若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、点P(m,0)是线段OB上的一个动点,过点P作y轴的平行线,交直线BC于D,交抛物线于E,EF∥x轴,交直线BC于F,DG∥x轴,FG∥y轴,DG与FG交于点G.设四边形DEFG的面积为S,当m为何值时S最大,最大值是多少?(3)、在坐标平面内是否存在点Q,将△OAC绕点Q逆时针旋转90°,使得旋转后的三角形恰好有两个顶点落在抛物线上.若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.