辽宁省抚顺县2017-2018学年八年级上学期数学期末考试试卷

试卷更新日期：2018-02-05 类型：期末考试

进入出卷网下载

一、单选题

1. 以下图标是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、2a+3b=5ab B、 ${(- l)}^{0}$ =1 C、 ${({ab}^{3})}^{2} = {ab}^{6}$ D、 ${(x + 2)}^{2}$ $= x^{2} + 4$

查看试题解析
3. 若分式 $\frac{2}{a + 1}$ 有意义，则a的取值范围是（）

A、a=0 B、a=1 C、a≠-1 D、a≠0

查看试题解析
4. 人体中红细胞的直径约为0.0000077m，将数0.0000077m用科学记数法表示为（）

A、7.7 $\times 10^{- 6}$ B、0.77 $\times 10^{- 7}$ C、77 $\times 10^{- 5}$ D、7.7 $\times 10^{- 7}$

查看试题解析
5. 若点M(a，-1)与点N(2，b)关于y轴对称，则a+b的值是（）

A、3 B、-3 C、1 D、-1

查看试题解析
6. 把多项式 $a^{2} - 4 a$ 分解因式的正确结果是（）

A、a(a - 4) B、(a+2)(a-2) C、a(a+2)(a-2) D、 ${(a - 2)}^{2}$ -4

查看试题解析
7. 已知关于x的分式方程 $\frac{m}{x - 1}$ =1的解是非负数，则m的取值范围是（）

A、m $\geq$ 1 B、m $\leq$ 1 C、m $\geq$ -1旦m≠0 D、m $\geq$ -1

查看试题解析
8. 如图，△ABC≌△ADE，∠DAC=60 $°$ ，∠BAE=100 $°$ ，BC，DE相交于点F，则∠DFB度数是（）

A、15 $°$ B、20 $°$ C、25 $°$ D、30 $°$

查看试题解析
9. 如图，在△ABC中，AB=AC，∠A=120 $°$ ，BC=6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为（）

A、1.5cm B、2cm C、2.5cm D、3cm

查看试题解析
10. 如图，AD是△ABC的角平分线，DE⊥AC垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF.给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF 正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知△ABC的两条边长分别是2和5，第三边c的取值范围是.

查看试题解析
12. 计算 $\frac{1}{a^{2} - 1} + \frac{a}{a^{2} - 1} =$ .

查看试题解析
13. 一个n边形的内角和是900 $°$ ，那么n=.

查看试题解析
14. 若 $x^{2} + mx + 9$ 是一个完全平方式，则m=.

查看试题解析
15. 已知 $a + b = 3$ ， $ab = - 2$ ，则 $a^{2} + b^{2}$ =.

查看试题解析
16. 在平面上将边长相等的正方形、正五边形和正六边形按如图所示的位置摆放，则 $∠ 1 =$ 度．

查看试题解析
17. 如图，四边形ABCD中，点M、N分别在AB、BC上，将∆BMN沿MN翻折，得∆FMN，若MF∥AD，FN∥DC，则∠D的度数为º

查看试题解析
18. 如图，等腰三角形ABC的底边BC长为4，面积是12，腰AB的垂直平分线EF分别交AB，AC于点E、F，若点D为底边BC的中点，点M为线段EF上一动点，则△BDM的周长的最小值为．

查看试题解析

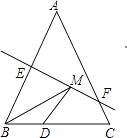
三、解答题

19. 计算

(1)、 ${(2 a^{2})}^{3} b^{3} \div 4 a^{3} b^{2}$

(2)、 $x^{2} (x + 1) - (x^{2} - 1) (x + 2)$ ．

查看试题解析
20. 先化简，再求值： $（ 1 - \frac{1}{a + 2} ） \div \frac{a^{2} - 1}{a + 2}$ ，其中a=3．

查看试题解析
21. 把下列多项式因式分解

(1)、 $x^{3} - 4 {xy}^{2}$ ；

(2)、 $(a - 1) (a + 3) + 4$

查看试题解析
22. 解方程： $\frac{2}{x - 3} = \frac{3}{x}$

查看试题解析
23. 已知：如图，△ABC.

(1)、分别画出与△ABC关于x轴、y轴对称的图形△A₁B₁C₁和△A₂B₂C₂；

(2)、写出△A₁B₁C₁和△A₂B₂C₂各顶点的坐标；

(3)、直接写出△ABC的面积，

查看试题解析
24. 如图，在△ABC中．AB=AC．∠BAC=90 $°$ ．E是AC边上的一点，延长BA至D，使AD=AE，连接DE，CD.

(1)、图中是否存在两个三角形全等？如果存在请写出哪两个三角形全等，并且证明；如果不存在，请说明理由；

(2)、若∠CBE=30 $°$ ，求∠ADC的度数.

查看试题解析
25. 某学校准备组织部分学生到当地社会实践基地参加活动，陈老师从社会实践基地带回来了两条信息：
信息一：按原来报名参加的人数，共需要交费用320元．现在报名参加的人数增加到原来人数的2倍，可以享受优惠，此时只需交费用480元；
信息二：享受优惠后，参加活动的每位同学平均分摊的费用比原来少4元．根据以上信息，现在报名参加的学生有多少人？

查看试题解析
26. 如图①，在等边三角形ABC中．D是AB边上的动点，以CD为一边，向上作等边三角形EDC．连接AE.

(1)、求证：△DBC≌△EAC

(2)、试说明AE∥BC的理由．

(3)、如图②，当图①中动点D运动到边BA的延长线上时，所作仍为等边三角形，猜想是否仍有AE∥BC?若成立请证明．

查看试题解析