内蒙古赤峰市宁城县2017-2018学年八年级上学期数学期末考试试卷

试卷更新日期：2018-02-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下面4个汽车标志图案，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列实际情景运用了三角形稳定性的是（）

A、人能直立在地面上 B、校门口的自动伸缩栅栏门 C、古建筑中的三角形屋架 D、三轮车能在地面上运动而不会倒

查看试题解析
3. 下列计算正确的是（）

A、a³·a⁴＝a¹² B、(a³)⁴＝a⁷ C、(a²b)³＝a⁶b³ D、a³÷a⁴＝a(a≠0)

查看试题解析
4. 不能用尺规作图作出唯一三角形的是（）

A、已知两角和夹边 B、已知两边和夹角 C、已知两角和其中一角的对边 D、已知两边和其中一边的对角

查看试题解析
5. 下列从左边到右边的变形，是因式分解的是（）

A、（3-x）（3+x）=9-x² B、x²+2x+1＝x(x+1)+1 C、a²b+ab²=ab（a+b） D、(a-b)(n-m)=(b-a)(n-m)

查看试题解析
6. 根据分式的基本性质可知， $\frac{a}{b}$ ＝ $\frac{()}{b^{2}}$ （）

A、a² B、b² C、ab D、ab²

查看试题解析
7. 如图所示，E，B，F，C四点在一条直线上，EB=CF，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是（）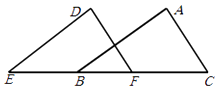

A、AB=DE B、DF∥AC C、∠E=∠ABC D、AB∥DE

查看试题解析
8. 将一副直角三角板如图放置，使含30°角的三角板的一条直角边和45°角的三角板的一条直角边重合，则∠1的度数为（）

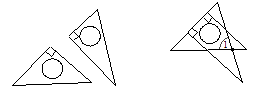A、45° B、60° C、75° D、85°

查看试题解析
9. 如图，OP平分∠AOB，PC⊥OA，PD⊥OB，垂足分别是C、D．下列结论中错误的是（）。

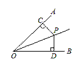A、PC = PD B、OC = OD C、∠CPO = ∠DPO D、OC = PC

查看试题解析
10. 在平面镜里看到背后墙上的电子钟示数如图所示，这时的实际时间应是（）

A、21：02 B、21：05 C、20：15 D、20：05

查看试题解析
11. 若关于x的方程 $\frac{3}{x - 1} = 1 - \frac{k}{1 - x}$ 有增根，则k的值为（）．

A、3 B、1 C、0 D、－1

查看试题解析
12. 已知：2+ $\frac{2}{3}$ =2²× $\frac{2}{3}$ ；3+ $\frac{3}{8}$ =3²× $\frac{3}{8}$ ；4+ $\frac{4}{15}$ =4²× $\frac{4}{15}$ ；5+ $\frac{5}{24}$ =5²× $\frac{5}{24}$ …，若10+ $\frac{b}{a}$ =10²× $\frac{b}{a}$ 符合前面式子的规律，则a+b=（）

A、99 B、109 C、100 D、120

查看试题解析

二、填空题

13. 请写出一个多项式（最多三项），使它能先“提公因式”，再“运用公式”来分解因式.你编写的多项式是：，分解因式的结果是.

查看试题解析
14. 由于自然环境的日益恶化，我们赖以生存的空气质量正在悄悄地变化。净化的空气的单位体积质量为0.00124g/cm³ ，将它用科学记数表示为g/cm³。

查看试题解析
15. 已知m²－2m－1=0，则代数式2m²－4m+2017的值为.

查看试题解析
16. 当三角形中一个内角α是另一个内角β的一半时，我们称此三角形为“半角三角形”，其中α称为“半角”．如果一个“半角三角形”的“半角”为25°，那么这个“半角三角形”的最大内角的度数为．

查看试题解析
17. 如图所示是小李绘制的某大桥断裂的现场草图，若∠1=38°，∠2=23°，则桥面断裂处夹角∠BCD为度．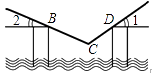

查看试题解析
18. 如图，小新从A点出发，沿直线前进50米后向左转30º，再沿直线前进50米，又向左转30º，……照这样下去，小新第一次回到出发地A点时，一共走了米。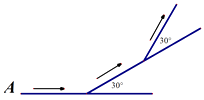

查看试题解析

三、解答题

19. 先化简再求值： $\frac{a^{2}}{a - 1} - a - 1$ ，其中a=2

查看试题解析
20. 解方程： $\frac{x}{x - 1} - 1 = \frac{3}{(x - 1) (x + 2)}$ ．

查看试题解析
21. 计算：

(1)、 $2^{- 1}$ +|﹣ $\frac{1}{2}$ |+（ $\frac{π}{3}$ ）⁰

(2)、已知：a+b＝4，ab ＝ 3，求：a²+b²的值。

查看试题解析
22. 如图所示，在直角坐标系xOy中，△ABC三点的坐标分别为A(－1，0)，B(－4，4)，C(0，3)．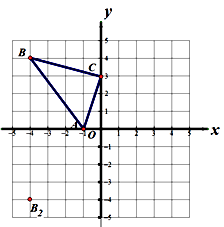

(1)、在图中画出△ABC关于y轴对称的图形△A₁B₁C₁；写出B₁的坐标为.

(2)、填空：在图中，若B₂(－4，－4)与点B关于一条直线成轴对称，则这条对称轴是，此时点C关于这条直线的对称点C₂的坐标为；

(3)、在y轴上确定一点P，使△APB的周长最小.(注：简要说明作法，保留作图痕迹，不求坐标)

查看试题解析
23. 某人驾车从A地到B地，出发2小时后车子出了点毛病，耽搁了半小时修车，为了弥补耽搁的时间他将车速增加到后来的1.6倍，结果按时到达，已知A、B两地相距100千米，求某人原来驾车的速度.

查看试题解析
24. 探究归纳题：

(1)、试验分析：
如图1，经过A点可以做条对角线；同样，经过B点可以做条；经过C点可以做条；经过D点可以做条对角线.
通过以上分析和总结，图1共有条对角线.

(2)、拓展延伸：
运用（1）的分析方法，可得：
图2共有条对角线；
图3共有条对角线；

(3)、探索归纳：
对于n边形(n>3)，共有条对角线．(用含n的式子表示)

(4)、特例验证：
十边形有对角线.

查看试题解析
25. 自学下面材料后，解答问题．
分母中含有未知数的不等式叫做分式不等式．如： $\frac{x - 2}{x + 1}$ ＞0； $\frac{2 x + 3}{x - 1}$ ＜0等．那么如何求出它们的解集呢？
根据我们学过的有理数除法法则可知：两数相除，同号得正，异号得负．其字母表达式为：

(1)、若a＞0，b＞0，则 $\frac{a}{b}$ ＞0；若a＜0，b＜0，则 $\frac{a}{b}$ ＞0；解不等式 $\frac{x - 2}{x + 1}$ ＜0.

(2)、若a＞0，b＜0，则 $\frac{a}{b}$ ＜0；若a＜0，b＞0，则 $\frac{a}{b}$ ＜0.
反之：①若 $\frac{a}{b}$ ＞0，则 ${\begin{matrix} a > 0 \\ b > 0 \end{matrix}$ 或 ${\begin{matrix} a < 0 \\ b < 0 \end{matrix}$ ，
②若 $\frac{a}{b}$ ＜0，则 ${\begin{matrix} a > 0 \\ b > 0 \end{matrix}$ 或 ${\begin{matrix} a < 0 \\ b < 0 \end{matrix}$ ．
根据上述规律，①求不等式 $\frac{x - 2}{x + 1}$ < 0的解集．
②直接写出不等式解集为x>3或x<1的最简分式不等式.

查看试题解析
26. 已知，如图1：△ABC中，∠B、∠C的平分线相交于点O，过点O作EF∥BC交AB、AC于E、F．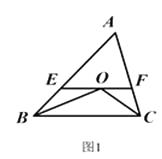

(1)、直接写出图1中所有的等腰三角形，并指出EF与BE、CF间有怎样的数量关系？

(2)、在（1）的条件下，若AB=10，AC=15，求△AEF的周长．

(3)、如图2，若△ABC中，∠B的平分线与三角形外角∠ACG的平分线CO交于点O，过O点作OE∥BC交AB于E，交AC于F，请问（1）中EF与BE、CF间的关系还是否存在，若存在，说明理由；若不存在，写出三者新的数量关系，并说明理由．

查看试题解析