北京八十五中2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期：2018-02-02 类型：期末考试
一、单选题
-
1. 下列图案属于轴对称图形的是（ ）A、
B、
C、
D、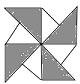
2. 点M（1，2）关于y轴对称点的坐标为（ ）A、（﹣1，2） B、（﹣1，﹣2） C、（1，﹣2） D、（2，﹣1）3. 已知三角形两边长分别为7、11，那么第三边的长可以是（ ）A、2 B、3 C、4 D、54. 下列计算正确的是（ ）A、（a3）2=a6 B、a•a2=a2 C、a3+a2=a6 D、（3a）3=9a35. 一个多边形每个外角都等于36°，则这个多边形是几边形（ ）
A、7 B、8 C、9 D、106. 如图，已知△ABC中，∠A=75°，则∠1+∠2=（ ）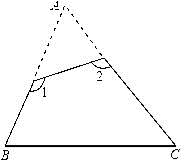
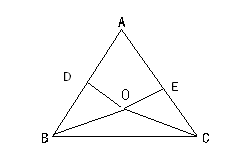
A、335°° B、255° C、155° D、150°7. 下列从左到右的运算是因式分解的是（ ）A、2a2﹣2a+1=2a（a﹣1）+1 B、（x﹣y）（x+y）=x2﹣y2 C、9x2﹣6x+1=（3x﹣1）2 D、x2+y2=（x﹣y）2+2xy8. 若等腰三角形的两边长分别为6和8，则周长为（ ）A、20或22 B、20 C、22 D、无法确定9. 已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是 （ ）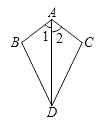
A、AB＝AC B、BD＝CD C、∠B＝∠C D、∠BDA＝∠CDA10. 如图，已知∠MON=30°，点A1 ， A2 ， A3 ， …在射线ON上，点B1 ， B2 ， B3 ， …在射线OM上，△A1B1A2 ， △A2B2A3 ， △A3B3A4 ， …均为等边三角形，若OA1=2，则△A5B5A6的边长为（ ）
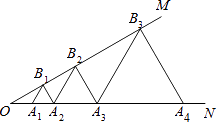A、8 B、16 C、24 D、32二、填空题
-
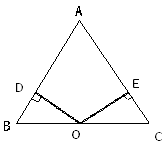
11. 科学家发现一种病毒的直径为0.0043微米，则用科学记数法表示为微米．12. 若一个三角形三个内角的度数之比为1：2：3，则这个三角形中的最大的角度是 ．13. 计算（π﹣3.14）0+ = ．14. 若x2+mx+4是完全平方式，则m= ．15. 如图，∠AOB=30°，OP平分∠AOB，PD⊥OB于D，PC∥OB交OA于C，若PC=6，则PD= ．
16. 下面的图表是我国数学家发明的“杨辉三角”，此图揭示了（a+b）n（n为非负整数）的展开式的项数及各项系数的有关规律．请你观察，并根据此规律写出：（a﹣b）5= ．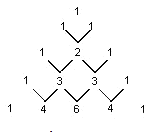
，
，
，
，
三、解答题
-
17. 计算：
(1)、（﹣a2）3•4a(2)、2x（x+1）+（x+1）2 ．18. 解下列分式方程：
(1)、(2)、 ．19. 看图回答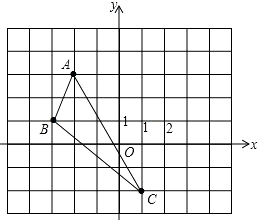
①画出△ABC关于y轴对称的图形△A1B1C1；
②在x轴上找出点P，使得点P到点A、点B的距离之和最短（保留作图痕迹）
20. 如图，点E、F在BC上，BE=FC，AB=DC，∠B=∠C．求证：∠A=∠D．
21. 小鹏的家距离学校1600米，一天小鹏从家去上学，出发10分钟后，爸爸发现他的数学课本忘了拿，立即带上课本去追他，在学校门口追上了他，已知爸爸的速度是小鹏速度的2倍，求小鹏的速度．22. 如图，在△ABC中，AB=AC，∠A=36°，DE是AC的垂直平分线．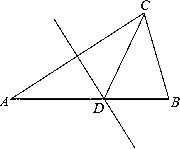
(1)、求证：△BCD是等腰三角形；(2)、△BCD的周长是a，BC=b，求△ACD的周长（用含a，b的代数式表示）23. 先化简代数式： ，然后再从﹣2≤x≤2的范围内选取一个合适的整数代入求值．
