福建省泉州市2018届高中毕业班1月文数质量检查试卷
试卷更新日期:2018-02-01 类型:高考模拟
一、单选题
-
1. 已知复数 满足 ,则其共轭复数 ( )A、 B、 C、 D、2. 若集合 有且只有一个元素,则实数 的取值范围为( )A、 B、 C、 D、3. 已知等比数列 是递增数列, ,则公比 ( )
A、 B、 C、 D、4. 已知 ,则( )A、 B、 C、 D、5. 设数列 的前 项和 ,若 ,则 ( )A、 B、 C、 D、6. 已知函数 ,则( )A、 的周期为 ,其图象关于直线 对称 B、 的周期为 ,其图象关于直线 对称 C、 的周期为 ,其图象关于直线 对称 D、 的周期为 ,其图象关于直线 对称7. 执行如图所示的程序框图,如果输入的 ,则输出的 ( )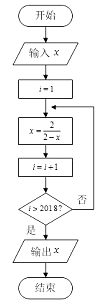 A、 B、 C、 D、8. 在直角坐标系 中, 为单位圆 上不同的两点, 的横坐标为 ,若 ,则 的横坐标是( )
A、 B、 C、 D、8. 在直角坐标系 中, 为单位圆 上不同的两点, 的横坐标为 ,若 ,则 的横坐标是( )
A、 B、 或 C、 D、 或9. 如图,网格纸上小正方形的边长为 ,粗线画出的是某几何体的三视图,则该几何体的体积为( )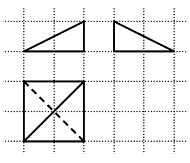 A、 B、 C、 D、10. 实数 满足 ,则 的最大值为( )A、 B、 C、 D、11. 设点 为双曲线 的左右焦点,点 为 右支上一点,点 为坐标原点,若 是底角为 的等腰三角形,则 的离心率为( )A、 B、 C、 D、12. 设函数 ,若不等式 恰有两个整数解,则实数 的取值范围是 ( )A、 B、 C、 D、
A、 B、 C、 D、10. 实数 满足 ,则 的最大值为( )A、 B、 C、 D、11. 设点 为双曲线 的左右焦点,点 为 右支上一点,点 为坐标原点,若 是底角为 的等腰三角形,则 的离心率为( )A、 B、 C、 D、12. 设函数 ,若不等式 恰有两个整数解,则实数 的取值范围是 ( )A、 B、 C、 D、二、填空题
-
13. 已知向量 满足 ,则 .14. 若函数 ,则 .15. 若二次函数 的最小值为 ,则 的取值范围为 .
16. 在三棱锥 中, ,若三棱锥的所有顶点,都在同一球面上,则球的表面积是 .三、解答题
-
17. 在平面直角坐标系 中,点 在抛物线 上.
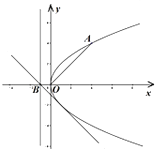 (1)、求 的方程和 的焦点的坐标;(2)、设点 为准线与 轴的交点,直线 过点 ,且与直线 垂直,求证: 与 相切.18. 等差数列 的前 项和为 ,已知 .(1)、求 的通项公式;(2)、求数列 的前 项和.19. 已知 分别为 内角的对边 , .
(1)、求 的方程和 的焦点的坐标;(2)、设点 为准线与 轴的交点,直线 过点 ,且与直线 垂直,求证: 与 相切.18. 等差数列 的前 项和为 ,已知 .(1)、求 的通项公式;(2)、求数列 的前 项和.19. 已知 分别为 内角的对边 , .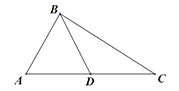 (1)、若 为 的中点,求 ;(2)、若 ,判断 的形状,并说明理由.
(1)、若 为 的中点,求 ;(2)、若 ,判断 的形状,并说明理由.