上海市静安区2017-2018学年高三上学期数学教学质量检测试卷
试卷更新日期:2018-02-01 类型:期末考试
一、单选题
-
1. “抛物线 的准线方程为 ”是“抛物线 的焦点与双曲线 的焦点重合”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件2. 已知等比数列 前 项和为 ,则下列一定成立的是( )A、若 ,则 ; B、若 ,则 ; C、若 ,则 ; D、若 ,则 .3. 某班班会准备从含甲、乙的6名学生中选取4人发言,要求甲、乙两人至少有一人参加,那么不同的发言顺序有( )A、336种 B、320种 C、192种 D、144种4. 已知椭圆 抛物线 焦点均在 轴上, 的中心和 顶点均为原点 ,从每条曲线上各取两个点,将其坐标记录于表中,则 的左焦点到 的准线之间的距离为( )
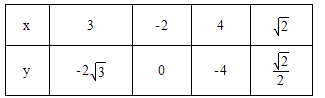 A、 B、 C、1 D、25. 对于集合 ,定义了一种运算“ ”,使得集合 中的元素间满足条件:如果存在元素 ,使得对任意 ,都有 ,则称元素 是集合 对运算“ ”的单位元素.例如: ,运算“ ”为普通乘法;存在 ,使得对任意 ,都有 ,所以元素 是集合 对普通乘法的单位元素.
A、 B、 C、1 D、25. 对于集合 ,定义了一种运算“ ”,使得集合 中的元素间满足条件:如果存在元素 ,使得对任意 ,都有 ,则称元素 是集合 对运算“ ”的单位元素.例如: ,运算“ ”为普通乘法;存在 ,使得对任意 ,都有 ,所以元素 是集合 对普通乘法的单位元素.下面给出三个集合及相应的运算“ ”:
② ,运算“ ”为普通减法;
② 表示 阶矩阵, },运算“ ”为矩阵加法;
③ (其中 是任意非空集合),运算“ ”为求两个集合的交集.
其中对运算“ ”有单位元素的集合序号为( )
A、①② B、①③ C、①②③ D、②③二、填空题
-
6. 若复数 ( 是虚数单位)是纯虚数,则实数 .
7. 若 为 上的奇函数,当 时, ,则 .8. 一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是9. 在菱形 中, , , 为 的中点,则 的值是;
10. 用半径1米的半圆形薄铁皮制作圆锥型无盖容器,其容积为立方米.11. 已知 为锐角,且 ,则 .12. 设函数 ,若存在 同时满足以下条件:①对任意的 ,都有 成立;② ,则 的取值范围是 .13. 若不等式 的解集是区间 的子集,则实数 的取值范围为 .14. 已知 且 , ), ,若对任意实数 均有 ,则 的最小值为 .15. 如图,正方形 的边长为2, 为 的中点,射线 从 出发,绕着点 顺时针方向旋转至 ,在旋转的过程中,记 为 , 所经过的在正方形 内的区域(阴影部分)的面积 ,那么对于函数 有以下三个结论:
① ;② 对任意 ,都有 ;
③ 对任意 ,且 ,都有 ;
其中所有正确结论的序号是;
三、解答题
-
16. 将边长为 的正方形 (及其内部)绕 旋转一周形成圆柱,如图, 长为 , 长为 ,其中 与 在平面 的同侧.
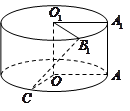 (1)、求三棱锥 的体积;(2)、求异面直线 与 所成的角的大小.17. 设双曲线 : , 为其左右两个焦点.(1)、设 为坐标原点, 为双曲线 右支上任意一点,求 的取值范围;(2)、若动点 与双曲线 的两个焦点 的距离之和为定值,且 的最小值为 ,求动点 的轨迹方程.18. 如图,在海岸线 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段 ,该曲线段是函数 , 的图像,图像的最高点为 .边界的中间部分为长1千米的直线段 ,且 .游乐场的后一部分边界是以 为圆心的一段圆弧 .
(1)、求三棱锥 的体积;(2)、求异面直线 与 所成的角的大小.17. 设双曲线 : , 为其左右两个焦点.(1)、设 为坐标原点, 为双曲线 右支上任意一点,求 的取值范围;(2)、若动点 与双曲线 的两个焦点 的距离之和为定值,且 的最小值为 ,求动点 的轨迹方程.18. 如图,在海岸线 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段 ,该曲线段是函数 , 的图像,图像的最高点为 .边界的中间部分为长1千米的直线段 ,且 .游乐场的后一部分边界是以 为圆心的一段圆弧 .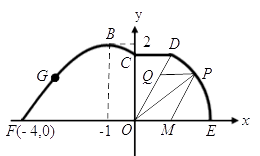 (1)、求曲线段 的函数表达式;
(1)、求曲线段 的函数表达式;
(2)、曲线段 上的入口 距海岸线 最近距离为1千米,现准备从入口 修一条笔直的景观路到 ,求景观路 长;(3)、如图,在扇形 区域内建一个平行四边形休闲区 ,平行四边形的一边在海岸线 上,一边在半径 上,另外一个顶点P在圆弧 上,且 ,求平行四边形休闲区 面积的最大值及此时 的值.19. 设集合 存在正实数 ,使得定义域内任意 都有 .(1)、若 ,试判断 是否为 中的元素,并说明理由;(2)、若 ,且 ,求 的取值范围;(3)、若 ( ),且 ,求 的最小值.20. 设数列 满足:① ;②所有项 ;③ .设集合 ,将集合 中的元素的最大值记为 .换句话说, 是
数列 中满足不等式 的所有项的项数的最大值.我们称数列 为数列 的
伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(1)、若数列 的伴随数列为1,1,1,2,2,2,3,请写出数列 ;(2)、设 ,求数列 的伴随数列 的前100之和;(3)、若数列 的前 项和 (其中 常数),试求数列 的伴随数列 前 项和 .