江苏省盐城市盐都区西片2016-2017学年七年级下学期数学开学考试试卷
试卷更新日期：2018-01-30 类型：开学考试
一、单选题
-
1. 冰箱冷藏室的温度零上5℃，记作+5℃，保鲜室的温度零下7℃，记作（ ）A、7℃ B、-7℃ C、2℃ D、-12℃2. 计算-3×|-2|的结果等于（ ）A、6 B、5 C、-6 D、-53. 下列图形属于棱柱的有（ ）
A、2个 B、3个 C、4个 D、5个4. 下列各组的两个单项式中，属于同类项的是（ ）A、3m2n2与-m2n3 B、 xy与2yx2 C、53与a3 D、-32x2y2与-23x2y 25. 如图，小军同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是（ ）
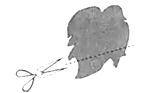A、垂线段最短 B、经过一点有无数条直线 C、经过两点，有且仅有一条直线 D、两点之间，线段最短6. 如图，OB平分∠AOD，OC平分∠BOD，∠BOC=15°，则∠AOC的度数为（ ）
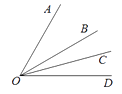A、75° B、60° C、45° D、30°7. 小李解关于x的方程5a-x=12时，误将-x看作+x，得方程的解为x=-3，则原方程的解是（ ）A、x=-2 B、x=1 C、x=3 D、x=28. 一张长方形桌子四周可坐6人，如果将一些相同的桌子按如图所示的方式拼桌子.若n张这样的长方形桌子拼在一起可以坐46人，则n等于（ ）
A、21 B、20 C、19 D、18二、填空题
-
9. 购买单价为a元的牛奶3盒，单价为b元的面包4个共需 元（用含有a、b的代数式表示）．10. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4400000000人，这个数用科学记数法表示为 ．11. 已知∠A=35°10′48″，则∠A的补角是°.12. 下列四种说法:
①过一点有且只有一条直线与已知直线平行；
②在同一平面内，两条不相交的线段是平行线段；
③相等的角是对顶角；
④在同一平面内，若直线AB∥CD，直线AB与EF相交，则CD与EF相交．
其中，错误的是（填序号）.
13. 如图是一个正方体的展开图，折叠成正方体后与“创”字相对的一面上的字是.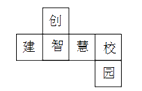
14. 如图是下午1点30分的钟面，则上午8点30分时刻，时钟的分针与时针所夹的角等于°．
15. 如图，两条直线相交成四个角，已知∠2＝3∠1，那么∠4＝°.
16. 某种商品的标价为200元，按标价的八折出售，这时仍可盈利25%，则这种商品的进价是元．17. 如图，是由一些小立方块所搭几何体的三种视图，若在所搭几何体的基础上（不改变原几何体中小立方块的位置），继续添加相同的小立方块，以搭成一个大正方体，至少还需要个小立方块．
三、计算题
-
18. 计算：
(1)、(-28 )-(-22)-(-17 )+(-22)；(2)、(-100)÷(-5)2-(- )×[34+(-32)].19. 计算：
(1)、5x2-2xy+4y2+xy-4y2-6x2；(2)、-3(3a2-2b2)-2(2a2+3b2).20. 解下列方程：
(1)、12-4(x-3)=7(x+5)；(2)、21. 已知a2+b2=5，ab=-2，求代数式2(4a2+2ab-b2)-3(5a2-3ab+2b2)+b2的值．四、解答题
-
22. 把边长为2厘米的6个相同正方体摆成如图的形式.
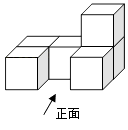(1)、画出该几何体的主视图、左视图、俯视图；
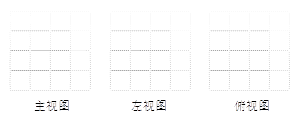(2)、试求出其表面积．
(3)、如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的左视图和俯视图不变，那么最多可以再添加个小正方体．
23. 如图，点P是∠AOB的边OB上的一点，过点P画OB的垂线，交OA于点C；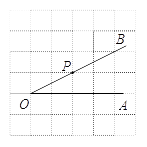
(1)、①过点C画OB的平行线CD；②过点P画OA的垂线，垂足为H；(2)、线段PH的长度是点P到的距离，线段的长度是点C到直线OB的距离．线段PC、PH、OC这三条线段大小关系是（用“＜”号连接）.24. 综合题
(1)、如图（1），将一副直角三角板的直角顶点C叠放在一起．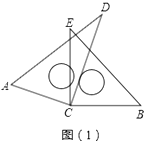
①填空：∠ACE∠BCD（选填“＜”或“＞”或“＝”）；
②若∠DCE=25°，求∠ACB的度数；
③猜想∠ACB与∠DCE的数量关系，并说明理由.
(2)、若改变（1）中一个三角板的位置，如图（2）所示，则上述第③题的结论是否仍然成立？（不需要说明理由）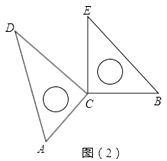
25. 有一笔钱，可以买甲种物品120件，或可以买乙种物品80件.现用这笔钱买了甲、乙两种物品共90件. 问甲、乙两种物品各买了多少件？26. 如图，点A从原点出发沿数轴向左运动，同时，点B也从原点出发沿数轴向右运动，4秒后，两点相距16个单位长度．已知点B的速度是点A的速度的3倍（速度单位：单位长度/秒）．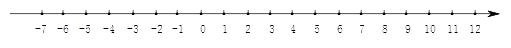
(1)、求出点A、点B运动的速度，并在数轴上标出A、B两点从原点出发运动4秒时的位置；(2)、若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动，再过几秒时，原点恰好处在AB的中点？(3)、若A、B两点从（1）中的位置开始，仍以原来的速度同时沿数轴向左运动时，另一点C同时从原点O位置出发向B点运动，且C的速度是点A的速度的一半；当点C运动几秒时，C为AB的中点？
27. 某人原计划用26天生产一批零件，工作两天后因改变了操作方法，每天比原来多生产5个零件结果提前4天完成任务，问原来每天生产多少个零件？这批零件有多少个？