浙江省杭州市萧山区临浦片2017届九年级下册数学开学考试试卷
试卷更新日期:2018-01-30 类型:开学考试
一、单选题
-
1. 的值为( )A、 B、 C、 D、12. 抛物线 的对称轴为( )A、直线 B、直线 C、直线 D、直线3. 掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得面朝上的点数是奇数的概率为( )。A、 B、 C、 D、4. 已知线段 ,则线段 的比例中项为( )A、 B、 C、 D、5. 将抛物线y=x2﹣2向左平移1个单位后再向上平移1个单位所得抛物线的表达式为( )A、 B、 C、 D、6. 圆内接正六边形的边长为3,则该圆内接正三角形的边长为( )A、 B、 C、 D、7. 已知抛物线 的对称轴为 ,交 轴的一个交点为( ,0),且 , 则下列结论:① , ;② ;③ ;④ . 其中正确的命题有( )个.A、1 B、2 C、3 D、48. 如图,在 的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点 ,则 的值为( )
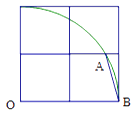 A、 B、2 C、 D、39. 如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为( )
A、 B、2 C、 D、39. 如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为( ) A、 B、 C、 D、10. 如图,顶角为36°的等腰三角形,其底边与腰之比等 ,这样的三角形称为黄金三角形,已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长( )
A、 B、 C、 D、10. 如图,顶角为36°的等腰三角形,其底边与腰之比等 ,这样的三角形称为黄金三角形,已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长( )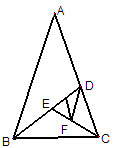 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知 ,则
12. 如图, 是半圆 的直径, ,则 的大小是度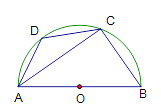 13. 抛物线 关于 轴对称的抛物线的解析式为14. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△EDF:S△BFC :S△BCD 等于
13. 抛物线 关于 轴对称的抛物线的解析式为14. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△EDF:S△BFC :S△BCD 等于 15. 已知一个直角三角形的一边长等于另一边长的2倍,那么这个直角三角形中较小锐角的正切值为16. 已知经过原点的抛物线 与 轴的另一个交点为 ,现将抛物线向右平移 个单位长度,所得抛物线与 轴交于 ,与原抛物线交于点 ,设 的面积为 ,则用 表示 =
15. 已知一个直角三角形的一边长等于另一边长的2倍,那么这个直角三角形中较小锐角的正切值为16. 已知经过原点的抛物线 与 轴的另一个交点为 ,现将抛物线向右平移 个单位长度,所得抛物线与 轴交于 ,与原抛物线交于点 ,设 的面积为 ,则用 表示 =
三、解答题
-
17. 甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)、请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)、求出两个数字之和能被3整除的概率.
18. 已知点 在⊙ 上, ,仅使用无刻度的直尺作图(保留痕迹)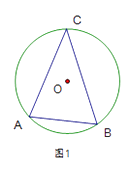
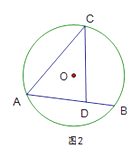 (1)、在图①中画一个含 的直角三角形;(2)、点 在弦 上,在图②中画一个含 的直角三角形.19. 某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ≈1.7)
(1)、在图①中画一个含 的直角三角形;(2)、点 在弦 上,在图②中画一个含 的直角三角形.19. 某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ≈1.7)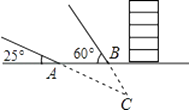 20. 已知:如图,在△ABC中,AB=AC=13,BC=24,点P、D分别在边BC、AC上,AP2=AD•AB,
20. 已知:如图,在△ABC中,AB=AC=13,BC=24,点P、D分别在边BC、AC上,AP2=AD•AB,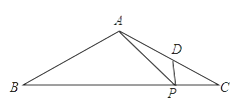 (1)、 ∽ ;(2)、求∠APD的正弦值.21. 给定关于 的二次函数 ,
(1)、 ∽ ;(2)、求∠APD的正弦值.21. 给定关于 的二次函数 ,学生甲:当 时,抛物线与 轴只有一个交点,因此当抛物线与 轴只有一个交点时, 的值为3;
学生乙:如果抛物线在 轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
22. 请完成以下问题: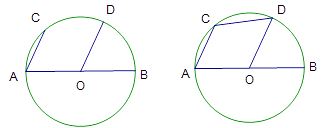
图1 图2
(1)、如图1, ,弦 与半径 平行,求证: 是⊙ 的直径;(2)、如图2, 是⊙ 的直径,弦 与半径 平行.已知圆的半径为 , , ,求 与 的函数关系式.23. 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).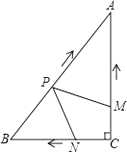 (1)、当t为何值时,以A,P,M为顶点的三角形与△ABC相似?(2)、是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
(1)、当t为何值时,以A,P,M为顶点的三角形与△ABC相似?(2)、是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.