浙江省湖州市长兴县2016届九年级下册数学开学考试试卷
试卷更新日期:2018-01-30 类型:开学考试
一、单选题
-
1. 二次函数y=x2+2x﹣3的图象与y轴的交点坐标是( )A、(0,﹣3) B、(﹣3,0) C、(1,0) D、(0,1)2. 如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )
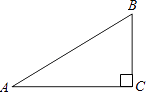 A、2 B、 C、 D、3. 在比例尺为1:100000的地图上,测得A,B两地之间的距离为2cm,则A,B两地之间的实际距离为( )A、200000cm B、400000cm C、200000000000cm D、400000000000cm4. 一个学习兴趣小组有4名女生,6名男生,现要从这10名学生中选出一人担当组长,则女生当组长的概率是( )A、 B、 C、 D、5.
A、2 B、 C、 D、3. 在比例尺为1:100000的地图上,测得A,B两地之间的距离为2cm,则A,B两地之间的实际距离为( )A、200000cm B、400000cm C、200000000000cm D、400000000000cm4. 一个学习兴趣小组有4名女生,6名男生,现要从这10名学生中选出一人担当组长,则女生当组长的概率是( )A、 B、 C、 D、5.如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
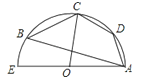 A、40° B、60° C、70° D、80°6. 将抛物线y=(x﹣1)2+1向下平移1个单位,所得新抛物线的解析式为( )A、y=(x﹣1)2+2 B、y=(x﹣1)2 C、y=(x﹣2)2+1 D、y=x2+17. 如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )
A、40° B、60° C、70° D、80°6. 将抛物线y=(x﹣1)2+1向下平移1个单位,所得新抛物线的解析式为( )A、y=(x﹣1)2+2 B、y=(x﹣1)2 C、y=(x﹣2)2+1 D、y=x2+17. 如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )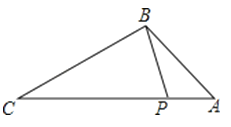 A、∠ABP=∠C B、∠APB=∠ABC C、AB2=AP•AC D、8. 如图,⊙O经过△ABC的两个顶点A,B,与边AC,BC分别交于点D,E,点P从点A出发,沿A→D→E→C的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图大致是( )
A、∠ABP=∠C B、∠APB=∠ABC C、AB2=AP•AC D、8. 如图,⊙O经过△ABC的两个顶点A,B,与边AC,BC分别交于点D,E,点P从点A出发,沿A→D→E→C的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图大致是( )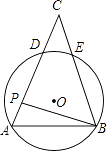 A、
A、 B、
B、 C、
C、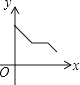 D、
D、 9. 如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )
9. 如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( ) A、b2>4ac B、ax2+bx+c≥﹣6 C、若点(﹣2,m),(﹣5,n)在抛物线上,则m>n D、关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣110. 如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN= ;③BP=4PK;④PM•PA=3PD2 , 其中正确的是( )
A、b2>4ac B、ax2+bx+c≥﹣6 C、若点(﹣2,m),(﹣5,n)在抛物线上,则m>n D、关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣110. 如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN= ;③BP=4PK;④PM•PA=3PD2 , 其中正确的是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
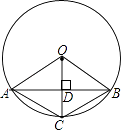
11. 计算:2cos60°﹣tan45°= .12. 二次函数y=x2+2x的顶点坐标为 , 对称轴是直线 .13. 如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是 .
 14. 如图,将两块直角三角形的一条直角边重合叠放,已知AC=BC= +1,∠D=60°,则两条斜边的交点E到直角边BC的距离是 .
14. 如图,将两块直角三角形的一条直角边重合叠放,已知AC=BC= +1,∠D=60°,则两条斜边的交点E到直角边BC的距离是 .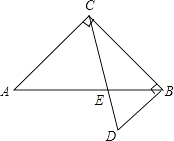 15. 若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为 .16. 如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则 的值为 .
15. 若等腰直角三角形的外接圆半径的长为2,则其内切圆半径的长为 .16. 如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则 的值为 .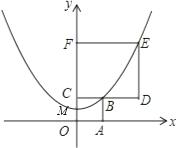
三、解答题
-
17. 在Rt△ABC中,已知∠C=90°,BC=6,cosB= ,求AC的长.
 18. 在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)、先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:
18. 在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.(1)、先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:事件A
必然事件
随机事件
m的值
(2)、先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于 ,求m的值.19. 综合题
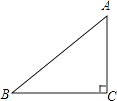
(1)、如图①,在△ABC中,点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,若AD=2,AE=1,DF=4,则EG= , = .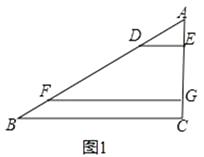 (2)、如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.
(2)、如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.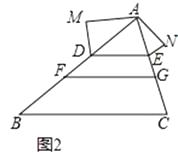 20. 如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.
20. 如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°. (1)、求a,b的值;(2)、连结OM,求∠AOM的大小.21. 已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)、求a,b的值;(2)、连结OM,求∠AOM的大小.21. 已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.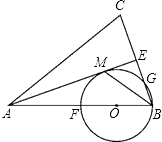 (1)、求证:AE与⊙O相切;
(1)、求证:AE与⊙O相切;
(2)、当BC=4,AC=6,求⊙O的半径.
22. 为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)、试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)、当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)、为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
23. 平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).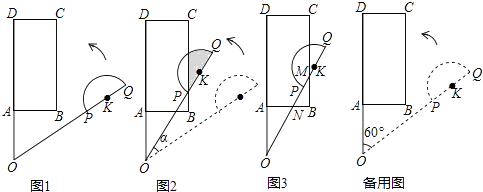
发现:如图2,当点P恰好落在BC边上时,求a的值即阴影部分的面积;
拓展:如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,直接写出sinα的值.
24. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠ACO= .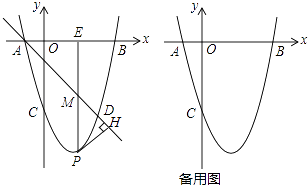 (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值;
(3)、在(2)的条件下,以点E为端点,在直线EP的右侧作一条射线与抛物线交于点N,使得∠NEP为锐角,在线段EB上是否存在点G,使得以E,N,G为顶点的三角形与△AOC相似?如果存在,请求出点G的坐标;如果不存在,请说明理由.