2016年云南省曲靖市中考数学试卷

试卷更新日期：2016-11-03 类型：中考真卷

进入出卷网下载

一、选择题

1. 4的倒数是（）

A、4 B、 $\frac{1}{4}$ C、﹣ $\frac{1}{4}$ D、﹣4

查看试题解析
2. 下列运算正确的是（）

A、3 $\sqrt{2}$ ﹣ $\sqrt{2}$ =3 B、a⁶÷a³=a² C、a²+a³=a⁵ D、（3a³）²=9a⁶

查看试题解析
3. 单项式x^m^﹣¹y³与4xyⁿ的和是单项式，则n^m的值是（）

A、3 B、6 C、8 D、9

查看试题解析
4. 实数a，b在数轴上对应点的位置如图所示，则下列结论正确的是（）

A、|a|＜|b| B、a＞b C、a＜﹣b D、|a|＞|b|

查看试题解析
5. 某校九年级体育模拟测试中，六名男生引体向上的成绩如下（单位：个）：10、6、9、11、8、10，下列关于这组数据描述正确的是（）

A、极差是6 B、众数是10 C、平均数是9.5 D、方差是16

查看试题解析
6. 小明所在城市的“阶梯水价”收费办法是：每户用水不超过5吨，每吨水费x元；超过5吨，每吨加收2元，小明家今年5月份用水9吨，共交水费为44元，根据题意列出关于x的方程正确的是（）

A、5x+4（x+2）=44 B、5x+4（x﹣2）=44 C、9（x+2）=44 D、9（x+2）﹣4×2=44

查看试题解析
7. 数如图，AD，BE，CF是正六边形ABCDEF的对角线，图中平行四边形的个数有（）

A、2个 B、4个 C、6个 D、8个

查看试题解析
8. 如图，C，E是直线l两侧的点，以C为圆心，CE长为半径画弧交l于A，B两点，又分别以A，B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧交于点D，连接CA，CB，CD，下列结论不一定正确的是（）

A、CD⊥l B、点A，B关于直线CD对称 C、点C，D关于直线l对称 D、CD平分∠ACB

查看试题解析

二、填空题

9. 计算： $\sqrt[3]{- 8}$ =

查看试题解析
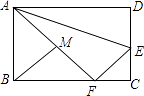
10. 如果整数x＞﹣3，那么使函数y= $\sqrt{π - 2 x}$ 有意义的x的值是（只填一个）

查看试题解析
11. 已知一元二次方程x²+mx+m﹣1=0有两个相等的实数根，则m= ．

查看试题解析
12. 如果一个圆锥的主视图是等边三角形，俯视图是面积为4π的圆，那么它的左视图的高是．

查看试题解析
13. 如图，在矩形ABCD中，AD=10，CD=6，E是CD边上一点，沿AE折叠△ADE，使点D恰好落在BC边上的F处，M是AF的中点，连接BM，则sin∠ABM= ．

查看试题解析
14. 等腰三角形ABC在平面直角坐标系中的位置如图所示，已知点A（﹣6，0），点B在原点，CA=CB=5，把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转，第一次翻转到位置①，第二次翻转到位置②…依此规律，第15次翻转后点C的横坐标是．

查看试题解析

三、解答题

15. $\sqrt{16}$ +（2﹣ $\sqrt{2}$ ）⁰﹣（﹣ $\frac{1}{2}$ ）^﹣²+|﹣1|

查看试题解析
16.
如图，已知点B，E，C，F在一条直线上，AB=DF，AC=DE，∠A=∠D．

(1)、求证：AC∥DE；

(2)、若BF=13，EC=5，求BC的长．

查看试题解析
17. 先化简： $\frac{x}{x + 3}$ ÷ $\frac{x^{2} + x}{x^{2} + 6 x + 9}$ + $\frac{3 x - 3}{x^{2} - 1}$ ，再求当x+1与x+6互为相反数时代数式的值．

查看试题解析
18. 如图，已知直线y₁=﹣ $\frac{1}{2}$ x+1与x轴交于点A，与直线y₂=﹣ $\frac{3}{2}$ x交于点B．

(1)、求△AOB的面积；

(2)、求y₁＞y₂时x的取值范围．

查看试题解析
19. 甲、乙两地相距240千米，一辆小轿车的速度是货车速度的2倍，走完全程，小轿车比货车少用2小时，求货车的速度．

查看试题解析
20. 根据频数分布表或频数分布直方图求加权平均数时，统计中常用各组的组中值代表各组的实际数据，把各组的频数看作相应组中值的权，请你依据以上知识，解决下面的实际问题．
为了解5路公共汽车的运营情况，公交部门统计了某天5路公共汽车每个运行班次的载客量，并按载客量的多少分成A，B，C，D四组，得到如下统计图：

(1)、求A组对应扇形圆心角的度数，并写出这天载客量的中位数所在的组；

(2)、求这天5路公共汽车平均每班的载客量；

(3)、如果一个月按30天计算，请估计5路公共汽车一个月的总载客量，并把结果用科学记数法表示出来．

查看试题解析
21. 在平面直角坐标系中，把横纵坐标都是整数的点称为“整点”．

(1)、直接写出函数y= $\frac{3}{x}$ 图象上的所有“整点”A₁ ， A₂ ， A₃ ， …的坐标；

(2)、在（1）的所有整点中任取两点，用树状图或列表法求出这两点关于原点对称的概率．

查看试题解析
22. 如图，在Rt△ABC中，∠BAC=90°，O是AB边上的一点，以OA为半径的⊙O与边BC相切于点E．

(1)、若AC=5，BC=13，求⊙O的半径；

(2)、过点E作弦EF⊥AB于M，连接AF，若∠F=2∠B，求证：四边形ACEF是菱形．

查看试题解析
23.
如图，在平面直角坐标系中，抛物线y=ax²+2ax+c交x轴于A，B两点，交y轴于点C（0，3），tan∠OAC= $\frac{3}{4}$ ．

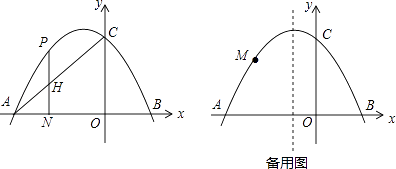(1)、求抛物线的解析式；

(2)、点H是线段AC上任意一点，过H作直线HN⊥x轴于点N，交抛物线于点P，求线段PH的最大值；

(3)、点M是抛物线上任意一点，连接CM，以CM为边作正方形CMEF，是否存在点M使点E恰好落在对称轴上？若存在，请求出点M的坐标；若不存在，请说明理由．

查看试题解析