2016年青海省中考数学试卷
试卷更新日期:2016-11-03 类型:中考真卷
一、填空题
-
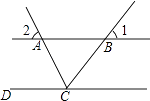
1. ﹣3的相反数是; 的立方根是 .2. 分解因式:2a2b﹣8b= , 计算:8x6÷4x2= .3. 据科学计算,我国广阔的陆地每年从太阳得到的能量相当于燃烧1248000000000000千克的煤所产生的能量,该数字用科学记数法表示为千克.4. 函数y= 的自变量x的取值范围是5. 如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2=
 6. 如图,已知∠CAE是△ABC的外角,AD∥BC,且AD是∠EAC的平分线,若∠B=71°,则∠BAC= .
6. 如图,已知∠CAE是△ABC的外角,AD∥BC,且AD是∠EAC的平分线,若∠B=71°,则∠BAC= .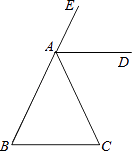 7. 如图,直线y= x与双曲线y= 在第一象限的交点为A(2,m),则k= .
7. 如图,直线y= x与双曲线y= 在第一象限的交点为A(2,m),则k= .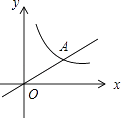 8. 如图,AC是汽车挡风玻璃前的雨刷器,如果AO=45cm,CO=5cm,当AC绕点O顺时针旋转90°时,则雨刷器AC扫过的面积为 cm2(结果保留π).
8. 如图,AC是汽车挡风玻璃前的雨刷器,如果AO=45cm,CO=5cm,当AC绕点O顺时针旋转90°时,则雨刷器AC扫过的面积为 cm2(结果保留π). 9. 已知一个围棋盒子中装有7颗围棋子,其中3颗白棋子,4颗黑棋子,若往盒子中再放入x颗白棋子和y颗黑棋子,从盒子中随机取出一颗白棋子的概率为 ,则y与x之间的关系式是 .10. 如图,在⊙O中,AB为直径,CD为弦,已知∠CAB=50°,则∠ADC= .
9. 已知一个围棋盒子中装有7颗围棋子,其中3颗白棋子,4颗黑棋子,若往盒子中再放入x颗白棋子和y颗黑棋子,从盒子中随机取出一颗白棋子的概率为 ,则y与x之间的关系式是 .10. 如图,在⊙O中,AB为直径,CD为弦,已知∠CAB=50°,则∠ADC= .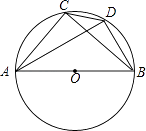 11. 如图,菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH= .
11. 如图,菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH= .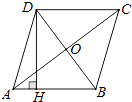 12.
12.如图,下列各图形中的三个数之间均具有相同的规律,依此规律,那么第4个图形中的x= , 一般地,用含有m,n的代数式表示y,即y= .

二、选择题
-
13. 下列运算正确的是( )A、a3+a2=2a5 B、(﹣ab2)3=a3b6 C、2a(1﹣a)=2a﹣2a2 D、(a+b)2=a2+b214. 以下图形中对称轴的数量小于3的是( )A、
 B、
B、 C、
C、 D、
D、 15. 不等式组 的解集在数轴上表示正确的是( )A、
15. 不等式组 的解集在数轴上表示正确的是( )A、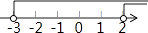 B、
B、 C、
C、 D、
D、 16. 已知等腰三角形的腰和底的长分别是一元二次方程x2﹣6x+8=0的根,则该三角形的周长为( )A、8 B、10 C、8或10 D、1217. 在“我的阅读生活”校园演讲比赛中,有11名学生参加比赛,他们决赛的最终成绩各不相同,其中一名学生想知道自己能否进入前6名,除了要了解自己的成绩外,还要了解这11名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数18. 穿越青海境内的兰新高铁极大地改善了沿线人民的经济文化生活,该铁路沿线甲,乙两城市相距480km,乘坐高铁列车比乘坐普通快车能提前4h到达,已知高铁列车的平均行驶速度比普通列车快160km/h,设普通列车的平均行驶速度为xkm/h,依题意,下面所列方程正确的是( )A、 ﹣ =4 B、 =4 C、 =4 D、 =419.
16. 已知等腰三角形的腰和底的长分别是一元二次方程x2﹣6x+8=0的根,则该三角形的周长为( )A、8 B、10 C、8或10 D、1217. 在“我的阅读生活”校园演讲比赛中,有11名学生参加比赛,他们决赛的最终成绩各不相同,其中一名学生想知道自己能否进入前6名,除了要了解自己的成绩外,还要了解这11名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数18. 穿越青海境内的兰新高铁极大地改善了沿线人民的经济文化生活,该铁路沿线甲,乙两城市相距480km,乘坐高铁列车比乘坐普通快车能提前4h到达,已知高铁列车的平均行驶速度比普通列车快160km/h,设普通列车的平均行驶速度为xkm/h,依题意,下面所列方程正确的是( )A、 ﹣ =4 B、 =4 C、 =4 D、 =419.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
 A、
A、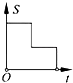 B、
B、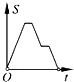 C、
C、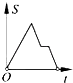 D、
D、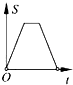 20. 如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S9的值为( )
20. 如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S9的值为( )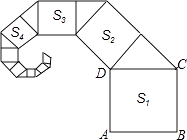 A、( )6 B、( )7 C、( )6 D、( )7
A、( )6 B、( )7 C、( )6 D、( )7三、解答题
-
21. 计算:﹣32+6cos45°﹣ +| ﹣3|22. 先化简,后求值:(x﹣ )÷ ,其中x=2+ .23. 如图,在▱ABCD中,点E,F在对角线AC上,且AE=CF.求证:
 (1)、DE=BF;(2)、四边形DEBF是平行四边形.24. 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
(1)、DE=BF;(2)、四边形DEBF是平行四边形.24. 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).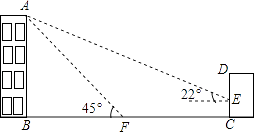 (1)、求办公楼AB的高度;(2)、若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(1)、求办公楼AB的高度;(2)、若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.(参考数据:sin22°≈ ,cos22° ,tan22 )
25. 如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.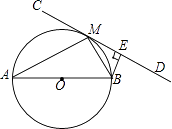 (1)、求证:∠BME=∠MAB;(2)、求证:BM2=BE•AB;(3)、若BE= ,sin∠BAM= ,求线段AM的长.26. 我省某地区为了了解2016年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如图1,如图2)
(1)、求证:∠BME=∠MAB;(2)、求证:BM2=BE•AB;(3)、若BE= ,sin∠BAM= ,求线段AM的长.26. 我省某地区为了了解2016年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如图1,如图2) (1)、填空:该地区共调查了 200 名九年级学生;(2)、将两幅统计图中不完整的部分补充完整;(3)、若该地区2016年初中毕业生共有3500人,请估计该地区今年初中毕业生中读普通高中的学生人数;(4)、老师想从甲,乙,丙,丁4位同学中随机选择两位同学了解他们毕业后的去向情况,请用画树状图或列表的方法求选中甲同学的概率.27.
(1)、填空:该地区共调查了 200 名九年级学生;(2)、将两幅统计图中不完整的部分补充完整;(3)、若该地区2016年初中毕业生共有3500人,请估计该地区今年初中毕业生中读普通高中的学生人数;(4)、老师想从甲,乙,丙,丁4位同学中随机选择两位同学了解他们毕业后的去向情况,请用画树状图或列表的方法求选中甲同学的概率.27.如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.
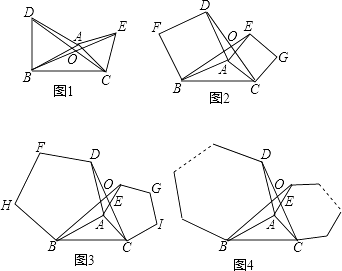 (1)、在图1中,求证:△ABE≌△ADC.(2)、由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.(3)、填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).(4)、由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示).28.
(1)、在图1中,求证:△ABE≌△ADC.(2)、由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.(3)、填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).(4)、由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示).28.如图1(注:与图2完全相同),二次函数y= x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
 (1)、求该二次函数的解析式;(2)、设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);(3)、若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).
(1)、求该二次函数的解析式;(2)、设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);(3)、若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).