2016年内蒙古呼伦贝尔市、兴安盟中考数学试卷

试卷更新日期：2016-11-03 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣ $\frac{1}{2}$ 的倒数为（）

A、﹣2 B、 $\frac{1}{2}$ C、﹣ $\frac{1}{2}$ D、2

查看试题解析
2. 化简（﹣x）³（﹣x）² ，结果正确的是（）

A、﹣x⁶ B、x⁶ C、x⁵ D、﹣x⁵

查看试题解析
3. 下列调查适合做抽样调查的是（）

A、对某小区的卫生死角进行调查 B、审核书稿中的错别字 C、对八名同学的身高情况进行调查 D、对中学生目前的睡眠情况进行调查

查看试题解析
4. 下列几何体中，主视图是矩形的是（）

A、 B、 C、 D、

查看试题解析
5. 某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（）

A、560（1+x）²=315 B、560（1﹣x）²=315 C、560（1﹣2x）²=315 D、560（1﹣x²）=315

查看试题解析
6. 将点A（3，2）向左平移4个单位长度得点A′，则点A′关于y轴对称的点的坐标是（）

A、（﹣3，2） B、（﹣1，2） C、（1，﹣2） D、（1，2）

查看试题解析
7. 如图，在△ABC中，AB=AC，过点A作AD∥BC，若∠1=70°，则∠BAC的大小为（）

A、40° B、30° C、70° D、50°

查看试题解析
8. 从一组数据中取出a个x₁ ， b个x₂ ， c个x₃ ，组成一个样本，那么这个样本的平均数是（）

A、 $\frac{x_{1} + x_{2} + x_{3}}{3}$ B、 $\frac{a x_{1} + a x_{2} + a x_{3}}{a + b + c}$ C、 $\frac{a x_{1} + a x_{2} + a x_{3}}{3}$ D、 $\frac{a + b + c}{3}$

查看试题解析
9. 若1＜x＜2，则 $| x - 3 | + \sqrt{{(x - 1)}^{2}}$ 的值为（）

A、2x﹣4 B、﹣2 C、4﹣2x D、2

查看试题解析
10. 园林队在某公园进行绿化，中间休息了一段时间，已知绿化面积S（m）²与工作时间t（h）的函数关系的图象如图所示，则休息后园林队每小时绿化面积为（）

A、100m² B、50m² C、80m² D、40m²

查看试题解析
11. 在平面直角坐标系中，将抛物线y=﹣ $\frac{1}{2}$ x²向下平移1个单位长度，再向左平移1个单位长度，得到的抛物线的解析式是（）

A、y=﹣ $\frac{1}{2}$ x²﹣x﹣ $\frac{3}{2}$ B、y=﹣ $\frac{1}{2}$ x²+x﹣ $\frac{1}{2}$ C、y=﹣ $\frac{1}{2}$ x²+x﹣ $\frac{3}{2}$ D、y=﹣ $\frac{1}{2}$ x²﹣x﹣ $\frac{1}{2}$

查看试题解析
12. 如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为PQ，则线段BQ的长度为（）

A、 $\frac{5}{3}$ B、 $\frac{5}{2}$ C、4 D、5

查看试题解析

二、填空题

13. 因式分解：xy²﹣4xy+4x= ．

查看试题解析
14. 一天有8.64×10⁴秒，一年如果按365天计算，用科学记数法表示一年有秒．

查看试题解析
15. 不等式组 ${\begin{matrix} 2 x - 1 > x + 1 \\ x + 8 < 4 x - 1 \end{matrix}$ 的解集是．

查看试题解析
16. 小杨用一个半径为36cm、面积为324πcm²的扇形纸板制作一个圆锥形的玩具帽（接缝的重合部分忽略不计），则帽子的底面半径为 cm．

查看试题解析
17. 如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′，A′C′交AB于点E，若AD=BE，则△A′DE的面积是．

查看试题解析

三、解答题

18. 计算：3tan30°﹣ $\frac{3}{\sqrt{3}}$ +（2016+π）⁰+（﹣ $\frac{1}{2}$ ）^﹣² ．

查看试题解析
19. 解方程： $\frac{3}{x - 1} - \frac{x + 3}{x^{2} - 1} = 0$ ．

查看试题解析
20. 如图，△ABC中，AD⊥BC，垂足是D，若BC=14，AD=12，tan∠BAD= $\frac{3}{4}$ ，求sinC的值．

查看试题解析
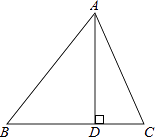21. 有甲、乙两个不透明的布袋，甲袋中有2个完全相同的小球，分别标有数字0个﹣2，；乙袋中有3个完全相同的小球，分别标有数字﹣2，0和1，小明从甲袋中随机取出1个小球，记录标有的数字为x，再从乙袋中随机取出1个小球，记录标有的数字为y，这样确定了点Q的坐标（x，y）

(1)、写出先Q所有可能的坐标；

(2)、求点Q在x轴上的概率．

查看试题解析
22. 如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE，已知：∠BAC=30°，EF⊥AB，垂足为F，连接DF．

(1)、试说明AC=EF；

(2)、求证：四边形ADFE是平行四边形．

查看试题解析
23. 为了解我市的空气质量情况，某环保兴趣小组从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）．
请你根据图中提供的信息，解答下列问题：

(1)、计算被抽取的天数；

(2)、请补全条形统计图，并求扇形统计图中表示“优”的扇形的圆心角度数；

(3)、请估计该市这一年（365天）达到“优”和“良”的总天数．

查看试题解析
24. 如图，已知⊙O的直径为AB，AC⊥AB于点A，BC与⊙O相交于点D，在AC上取一点E，使得ED=EA．

(1)、求证：ED是⊙O的切线；

(2)、当OE=10时，求BC的长．

查看试题解析
25. 某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体试验，测得成人服药后血液中药物浓度y（微克/毫升）与服药时间x小时之间函数关系如图所示（当4≤x≤10时，y与x成反比例）．

(1)、根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式．

(2)、问血液中药物浓度不低于4微克/毫升的持续时间多少小时？

查看试题解析
26.
如图，抛物线y=﹣x²+2x+3与x轴相交的于A，B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．

(1)、直接写出A，B，C三点的坐标和抛物线的对称轴；

(2)、连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点（P不与C，B两点重合），过点P作PF∥DE交抛物线于点F，设点P的横坐标为m．
①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形．
②设△BCF的面积为S，求S与m的函数关系式；当m为何值时，S有最大值．

查看试题解析