广东省深圳市龙岗区2017-2018学年八年级上学期数学期末考试试卷

试卷更新日期：2018-01-26 类型：期末考试

进入出卷网下载

一、选择题

1. 下列各数中是无理数的是（）

A、3.14 B、 $\frac{1}{3}$ C、 $\sqrt{36}$ D、 $- \sqrt{3}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ B、 $\sqrt{6} \div 2 = \sqrt{3}$ C、 $\sqrt{2} \cdot \sqrt{3} = \sqrt{6}$ D、 $\sqrt{8} = 4 \sqrt{2}$

查看试题解析
3. 以下列各组数据为边不能组成直角三角形的一组数据是（）

A、3,4,5 B、 $\frac{1}{3} ， \frac{1}{4} ， \frac{1}{5}$ C、6,8,10 D、5,12,13

查看试题解析
4.
如图，在数轴上表示实数 $\sqrt{15}$ 的点可能是（　　）

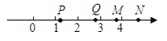A、点P B、点Q C、点M D、点N

查看试题解析
5. 点P（-3,5）关于x轴的对称点P^，的坐标是（）

A、（3,5） B、（5，-3） C、（3，-5） D、（-3，-5）

查看试题解析
6. 已知点P（x，y），且 $\sqrt{（ x - 2)^{2}} + | y + 4 | = 0$ ，则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 甲，乙，丙，丁四名跳远运动员选拔塞成绩的平均数 $\bar{a}$ 与方差 $s^{2}$ 如下表所示：

甲
乙
丙
丁
平均数 $\bar{a}$
561
561
560
560
方差 $s^{2}$
3.5
15.5
3.5
16.5
根据表中数据，要从中选一名成绩好又发挥稳定的运动员参赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 深圳空气质量优良指数排名近年来一直排在全国城市前十。下表是深圳市气象局于2016年3月22日在全市十一个监测点监测到空气质量指数（AQI）数据：
监测点
荔园
西乡
华侨城
南油
盐田
龙岗
洪湖
南澳
葵涌
梅沙
观澜
AQI
15
31
25
24
31
24
25
25
34
20
26
质量
优
优
优
优
优
优
优
优
优
优
优
上述（AQI）数据中，众数和中位数分别是（）

A、25,25 B、31,25 C、25,24 D、31,24

查看试题解析
9. 下列命题是假命题的为（）

A、如果三角形三个内角的比是1：2：3，那么这个三角形是直角三角形 B、锐角三角形的所有外角都是钝角 C、内错角相等 D、平行于同一直线的两条直线平行

查看试题解析
10. 2015年是国际“光”年，某校“光学节”纪念品是一个底面为等边三角形的三棱镜（如图）。三棱镜的三个侧面上，从顶点A到顶点A^，镶有一圈金属丝，已知此三棱镜的高为8cm，底面边为2cm，则这圈金属丝的长度至少为（）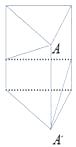

A、8cm B、10cm C、12cm D、15cm

查看试题解析
11. 如图所示，直线 $y = k (x - 2) + k - 1$ 与x轴、y轴分别交于B、C两点，且 $\frac{O B}{O C} = \frac{1}{2}$ 。则K的值为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
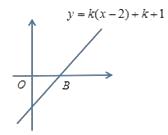12. 如图，A，B的坐标为（1，0），（0，2），若将线段AB平移至A₁B₁ ，则 $a - b$ 的值为（）

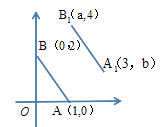A、 1 B、 -1 C、0 D、 2

查看试题解析

二、填空题

13. 已知一组数据：15，13,15，16,17，16，12，15，则极差为；

查看试题解析
14. 已知直角三角形的斜边长为6.5cm，一直角边为6cm则另一条直角边为cm

查看试题解析
15. 如图，函数 $y = 2 x + b$ 与函数 $y = k x - 1$ 的图象交干点P关于x的方程 $k x - 1 = 2 x + b$ 的解是；

查看试题解析
16. 如图，正方形OABC的顶点O在坐标原点，正方形ADEF的边AD与AB在同一宜线上，AF与0A在同一直线上，且AB=AD，0A边和AB边所在直线的解析式分别为： $y = \frac{3}{4} x$ 和 $y = - \frac{4}{3} x + \frac{25}{3}$ ，则点E的坐标为；

查看试题解析

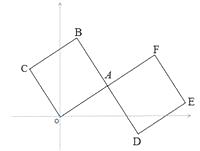
三、解答题

17. 计算：二次根式的化简与计算.

(1)、化简： $2 \sqrt{12} - 4 \sqrt{\frac{1}{8}} + 3 \sqrt{48}$

(2)、化简； $\sqrt{0.49} - \sqrt[3]{\frac{7}{8} - 1} - \sqrt{（ - 3 ）^{2}}$

查看试题解析
18. 解二元一次方程组

(1)、解方程组： ${\begin{cases} x + y = 7,① \\ 2 x + 4 y = 16②. \end{cases}$

(2)、解方程组： ${\begin{cases} 3 x - 4 y = 4① \\ \frac{x}{2} + \frac{y}{3} = 3② \end{cases}$

查看试题解析
19. 如图是甲、乙、丙三人百米赛跑的函数图象，根据右图回答下面问题；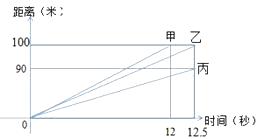

(1)、在这次比赛中，获得冠军：

(2)、甲比乙提前秒到达目的地；

(3)、乙的速度比丙快米/秒.

查看试题解析
20. 如图，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，∠BAD=80°，试求：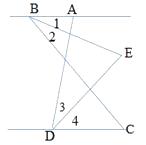

(1)、∠EDC的度数；

(2)、若∠BCD=n°，试求∠BED的度数。(用含n的式子表示）

查看试题解析
21. 如图，直线 $y = k x + 8$ 分别与x轴，y轴相交于A，B两点，0为坐标原点，A点的坐标为(4，0)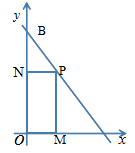

(1)、求k的值；

(2)、过线段AB上一点P(不与端点重合)作x轴，y轴的垂线，垂足分别为M，N。当长方形PMON的周长是10时，求点P的坐标。

查看试题解析
22. 小明到某服装专卖店去做社会调查，了解到该专卖店为了微励营业员的工作积极性，实行“月总收入=基本工资(固定)+计付奖金”的方法计算薪资，并获得如下信息；
营业员
小张
小王
月销售件数
200
150
月总收入/元
1400
1250
销售每件奖励a元，晋业员月基本工资为b元。

(1)、列方程组求a，b的值。

(2)、假设月销售件数为x，月总收入为y元，请写出y与x的函数关系式，并求出营业员小张上个月总收入是1700元时，小张上个月卖了多少件服装?

查看试题解析
23. 在x轴上有点P(a，0)（其中a>2)，过点P作x轴的垂线，分别交函数 $y = - \frac{1}{2} x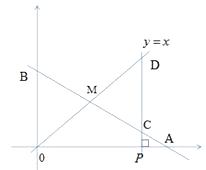 + b$ 和 $y = x$ 的图象于点C、D。

(1)、求点A的坐标

(2)、若OB=CD，求a的值

(3)、在(2)条件下若以0D线段为边，作正方形0DEF，求直线EF的表达式。

查看试题解析

	甲	乙	丙	丁
平均数 $\bar{a}$	561	561	560	560
方差 $s^{2}$	3.5	15.5	3.5	16.5

监测点	荔园	西乡	华侨城	南油	盐田	龙岗	洪湖	南澳	葵涌	梅沙	观澜
AQI	15	31	25	24	31	24	25	25	34	20	26
质量	优	优	优	优	优	优	优	优	优	优	优

营业员	小张	小王
月销售件数	200	150
月总收入/元	1400	1250