2016年辽宁省葫芦岛市中考数学试卷

试卷更新日期：2016-11-02 类型：中考真卷

进入出卷网下载

一、选择题

1. 4的相反数是（）

A、4 B、﹣4 C、 $\frac{1}{4}$ D、- $\frac{1}{4}$

查看试题解析
2. 下列运算正确的是（）

A、﹣a（a﹣b）=﹣a²﹣ab B、（2ab）²÷a²b=4ab C、2ab•3a=6a²b D、（a﹣1）（1﹣a）=a²﹣1

查看试题解析
3. 下列图形既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图是由5个相同的小正方体构成的几何体，其左视图是（）

A、 B、 C、 D、

查看试题解析
5. 九年级两名男同学在体育课上各练习10次立定跳远，平均成绩均为2.20米，要判断哪一名同学的成绩比较稳定，通常需要比较这两名同学立定跳远成绩的（）

A、方差 B、众数 C、平均数 D、中位数

查看试题解析
6. 下列一元二次方程中有两个相等实数根的是（）

A、2x²﹣6x+1=0 B、3x²﹣x﹣5=0 C、x²+x=0 D、x²﹣4x+4=0

查看试题解析
7. 在一个不透明的布袋中装有若干个只有颜色不同的小球，如果袋中有红球5个，黄球4个，其余为白球，从袋子中随机摸出一个球，“摸出黄球”的概率为 $\frac{1}{3}$ ，则袋中白球的个数为（）

A、2 B、3 C、4 D、12

查看试题解析
8. A，B两种机器人都被用来搬运化工原料，A型机器人比B型机器人每小时多搬运40千克，A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等．设B型机器人每小时搬运化工原料x千克，根据题意可列方程为（）

A、 $\frac{1200}{x + 40}$ = $\frac{800}{x}$ B、 $\frac{1200}{x - 40}$ = $\frac{800}{x}$ C、 $\frac{1200}{x}$ = $\frac{800}{x - 40}$ D、 $\frac{1200}{x}$ = $\frac{800}{x + 40}$

查看试题解析
9. 如图，在△ABC中，点D，E分别是边AB，AC的中点，AF⊥BC，垂足为点F，∠ADE=30°，DF=4，则BF的长为（）

A、4 B、8 C、2 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析
10. 甲、乙两车从A城出发前往B城，在整个行驶过程中，汽车离开A城的距离y（km）与行驶时间t（h）的函数图象如图所示，下列说法正确的有（）
①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时，乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 在“2016丝绸之路”国际投资贸易洽谈会上，我省销售的产品和合作项目签约金额为730000000元，将730000000用科学记数法表示为．

查看试题解析
12. 分解因式：a³﹣4a= ．

查看试题解析
13. 某广告公司全体员工年薪的具体情况如表：
年薪/万元
25
15
10
6
4
人数
1
1
3
3
2
则该公司全体员工年薪的中位数是万元．

查看试题解析
14. 如图，一只蚂蚁在正方形ABCD区域内爬行，点O是对角线的交点，∠MON=90°，OM，ON分别交线段AB，BC于M，N两点，则蚂蚁停留在阴影区域的概率为．

查看试题解析
15. 如图，A，B，C，D是⊙O上的四个点，∠C=110°，则∠BOD=度．

查看试题解析
16. 如图，四边形OABC为矩形，点A，C分别在x轴和y轴上，连接AC，点B的坐标为（4，3），∠CAO的平分线与y轴相交于点D，则点D的坐标为．

查看试题解析
17. 如图，在△AOB中，∠AOB=90°，点A的坐标为（2，1），BO=2 $\sqrt{5}$ ，反比例函数y= $\frac{k}{x}$ 的图象经过点B，则k的值为．

查看试题解析
18. 如图，点A₁（2，2）在直线y=x上，过点A₁作A₁B₁∥y轴交直线y= $\frac{1}{2}$ x于点B₁ ，以点A₁为直角顶点，A₁B₁为直角边在A₁B₁的右侧作等腰直角△A₁B₁C₁ ，再过点C₁作A₂B₂∥y轴，分别交直线y=x和y= $\frac{1}{2}$ x于A₂ ， B₂两点，以点A₂为直角顶点，A₂B₂为直角边在A₂B₂的右侧作等腰直角△A₂B₂C₂…，按此规律进行下去，则等腰直角△A_nB_nC_n的面积为（用含正整数n的代数式表示）

查看试题解析

三、解答题

19. 先化简：（2x﹣ $\frac{x^{2} + 1}{x}$ ）÷ $\frac{x^{2} - 2 x + 1}{x}$ ，然后从0，1，﹣2中选择一个适当的数作为x的值代入求值．

查看试题解析
20. 某学校计划开设四门选修课：乐器、舞蹈、绘画、书法．为提前了解学生的选修情况，学校采取随机抽样的方法进行问卷调查（每个被调查的学生必须选择而且只能选择其中一门）．对调查结果进行了整理，绘制成如下两幅不完整的统计图，请结合图中所给信息解答下列问题：

(1)、本次调查的学生共有人，在扇形统计图中，m的值是；

(2)、将条形统计图补充完整；

(3)、在被调查的学生中，选修书法的有2名女同学，其余为男同学，现要从中随机抽取2名同学代表学校参加某社区组织的书法活动，请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率．

查看试题解析
21. 在纪念中国抗日战争胜利70周年之际，某公司决定组织员工观看抗日战争题材的影片，门票有甲乙两种，甲种票比乙种票每张贵6元；买甲种票10张，乙种票15张共用去660元．

(1)、求甲、乙两种门票每张各多少元？

(2)、如果公司准备购买35张门票且购票费用不超过1000元，那么最多可购买多少张甲种票？

查看试题解析
22. 在一次课外实践活动中，同学们要测量某公园人工湖两侧A，B两个凉亭之间的距离．如图，现测得∠ABC=30°，∠CBA=15°，AC=200米，请计算A，B两个凉亭之间的距离（结果精确到1米）（参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
23. 如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交线段BC，AC于点D，E，过点D作DF⊥AC，垂足为F，线段FD，AB的延长线相交于点G．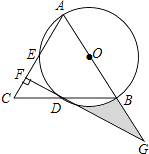

(1)、求证：DF是⊙O的切线；

(2)、若CF=1，DF= $\sqrt{3}$ ，求图中阴影部分的面积．

查看试题解析
24. 某文具店购进一批纪念册，每本进价为20元，出于营销考虑，要求每本纪念册的售价不低于20元且不高于28元，在销售过程中发现该纪念册每周的销售量y（本）与每本纪念册的售价x（元）之间满足一次函数关系：当销售单价为22元时，销售量为36本；当销售单价为24元时，销售量为32本．

(1)、请直接写出y与x的函数关系式；

(2)、当文具店每周销售这种纪念册获得150元的利润时，每本纪念册的销售单价是多少元？

(3)、设该文具店每周销售这种纪念册所获得的利润为w元，将该纪念册销售单价定为多少元时，才能使文具店销售该纪念册所获利润最大？最大利润是多少？

查看试题解析
25.
如图①，在△ABC中，∠BAC=90°，AB=AC，点E在AC上（且不与点A，C重合），在△ABC的外部作△CED，使∠CED=90°，DE=CE，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．

(1)、请直接写出线段AF，AE的数量关系；

(2)、将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论；

(3)、在图②的基础上，将△CED绕点C继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．

查看试题解析
26.
如图，抛物线y=﹣ $\frac{1}{2}$ x²+bx+c与x轴交于点A，点B，与y轴交于点C，点B坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点，过点D作x轴的垂线，垂足为E，连接BD．

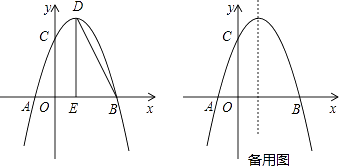(1)、求抛物线的解析式及点D的坐标；

(2)、点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；

(3)、若点M是抛物线上的动点，过点M作MN∥x轴与抛物线交于点N，点P在x轴上，点Q在平面内，以线段MN为对角线作正方形MPNQ，请直接写出点Q的坐标．

查看试题解析

年薪/万元	25	15	10	6	4
人数	1	1	3	3	2