2016年江苏省徐州市中考数学试卷
试卷更新日期:2016-11-02 类型:中考真卷
一、选择题
-
1. ﹣ 的相反数是( )A、4 B、﹣4 C、 D、﹣2. 下列运算中,正确的是( )A、x2+x3=x6 B、x3+x9=x27 C、(x2)3=x6 D、x÷x2=x33. 下列事件中的不可能事件是( )A、通常加热到100℃时,水沸腾 B、抛掷2枚正方体骰子,都是6点朝上 C、经过有交通信号灯的路口,遇到红灯 D、任意画一个三角形,其内角和是360°4. 下列图形中,不可以作为一个正方体的展开图的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下列图案中,是轴对称图形但不是中心对称图形的是( )A、
5. 下列图案中,是轴对称图形但不是中心对称图形的是( )A、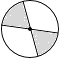 B、
B、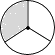 C、
C、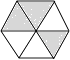 D、
D、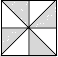 6. 某人一周内爬楼的层数统计如表
6. 某人一周内爬楼的层数统计如表周一
周二
周三
周四
周五
周六
周日
26
36
22
22
24
31
21
关于这组数据,下列说法错误的是( )
A、中位数是22 B、平均数是26 C、众数是22 D、极差是157. 函数y= 中自变量x的取值范围是( )A、x≤2 B、x≥2 C、x<2 D、x≠28. 如图是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )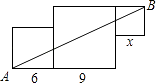 A、1或9 B、3或5 C、4或6 D、3或6
A、1或9 B、3或5 C、4或6 D、3或6二、填空题
-
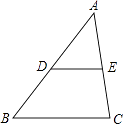
9. 某市2016年中考考生约为61500人,该人数用科学记数法表示为 .10. 若反比例函数的图象过点(3,﹣2),则其函数表达式为 .11. 若二次函数y=x2+2x+m的图象与x轴没有公共点,则m的取值范围是12. 如图,△ABC中,D、E分别为AB、AC的中点,则△ADE与△ABC的面积比为 .
 13. 若等腰三角形的顶角为120°,腰长为2cm,则它的底边长为 cm.14. 如图,⊙O是△ABC的内切圆,若∠ABC=70°,∠ACB=40°,则∠BOC=°.
13. 若等腰三角形的顶角为120°,腰长为2cm,则它的底边长为 cm.14. 如图,⊙O是△ABC的内切圆,若∠ABC=70°,∠ACB=40°,则∠BOC=°. 15. 用一个半径为10的半圆,围成一个圆锥的侧面,该圆锥的底面圆的半径为 .16. 如图,每个图案都由大小相同的正方形组成,按照此规律,第n个图案中这样的正方形的总个数可用含n的代数式表示为 .
15. 用一个半径为10的半圆,围成一个圆锥的侧面,该圆锥的底面圆的半径为 .16. 如图,每个图案都由大小相同的正方形组成,按照此规律,第n个图案中这样的正方形的总个数可用含n的代数式表示为 .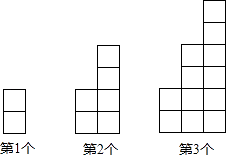 17. 如图,正方形ABCD的边长为2,点E,F分别在边AD,CD上,若∠EBF=45°,则△EDF的周长等于 .
17. 如图,正方形ABCD的边长为2,点E,F分别在边AD,CD上,若∠EBF=45°,则△EDF的周长等于 .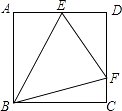
三、解答题
-
18. 计算:(1)、(﹣1)2016+x0﹣ +(2)、 ÷ .19. 解答(1)、解方程: +1= ;(2)、解不等式组: .20. 某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错的题目进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:
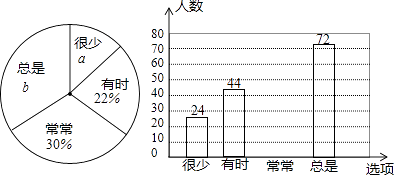
请根据图中信息,解答下列问题
(1)、该调查的样本容量为 , a=%,b=%,“常常”对应扇形的圆心角为°(2)、请你补全条形统计图;(3)、若该校共有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名?21. 某乳品公司最近推出一款果味酸奶,共有红枣、木瓜两种口味,若送奶员连续三天,每天从中任选一瓶某种口味的酸奶赠送给某住户品尝,则该住户收到的三瓶酸奶中,至少有两瓶为红枣口味的概率是多少?(请用“画树状图”的方法给出分析过程,并求出结果)
22. 如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长,交DC于点F,求证: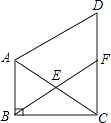 (1)、△ABE≌△CFE;(2)、四边形ABFD是平行四边形.23. 小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:(1)、小丽买了自动铅笔、记号笔各几支?(2)、若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
(1)、△ABE≌△CFE;(2)、四边形ABFD是平行四边形.23. 小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:(1)、小丽买了自动铅笔、记号笔各几支?(2)、若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?商品名
单价(元)
数量(个)
金额(元)
签字笔
3
2
6
自动铅笔
1.5
●
●
记号笔
4
●
●
软皮笔记本
●
2
9
圆规
3.5
1
●
合计
8
28
24. 如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m (1)、求点D到CA的距离;(2)、求旗杆AB的高.
(1)、求点D到CA的距离;(2)、求旗杆AB的高.(注:结果保留根号)
25. 某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与其价格x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:x(元)
180
260
280
300
y(间)
100
60
50
40
(1)、求y与x之间的函数表达式;(2)、已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出)26. 如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N (1)、若CM=x,则CH=(用含x的代数式表示);(2)、求折痕GH的长.27. 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣ ),C(2,0),其对称轴与x轴交于点D
(1)、若CM=x,则CH=(用含x的代数式表示);(2)、求折痕GH的长.27. 如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣ ),C(2,0),其对称轴与x轴交于点D (1)、求二次函数的表达式及其顶点坐标;(2)、若P为y轴上的一个动点,连接PD,则 PB+PD的最小值为;(3)、M(x,t)为抛物线对称轴上一动点
(1)、求二次函数的表达式及其顶点坐标;(2)、若P为y轴上的一个动点,连接PD,则 PB+PD的最小值为;(3)、M(x,t)为抛物线对称轴上一动点
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.