2016年贵州省黔西南州中考数学试卷
试卷更新日期:2016-11-02 类型:中考真卷
一、选择题:
-
1. 计算﹣42的结果等于( )A、﹣8 B、﹣16 C、16 D、82. 如图,△ABC的顶点均在⊙O上,若∠A=36°,则∠BOC的度数为( )
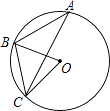 A、18° B、36° C、60° D、72°3. 如图,AB∥CD,CB∥DE,若∠B=72°,则∠D的度数为( )
A、18° B、36° C、60° D、72°3. 如图,AB∥CD,CB∥DE,若∠B=72°,则∠D的度数为( )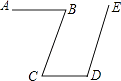 A、36° B、72° C、108° D、118°4. 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A、36° B、72° C、108° D、118°4. 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )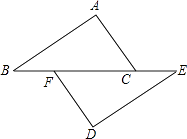 A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC5. 如图,在△ABC中,点D在AB上,BD=2AD,DE∥BC交AC于E,则下列结论不正确的是( )
A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC5. 如图,在△ABC中,点D在AB上,BD=2AD,DE∥BC交AC于E,则下列结论不正确的是( )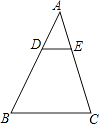 A、BC=3DE B、 = C、△ADE~△ABC D、S△ADE= S△ABC6. 甲、乙、丙三人站成一排拍照,则甲站在中间的概率是( )A、 B、 C、 D、7. 某校在国学文化进校园活动中,随机统计50名学生一周的课外阅读时间如表所示,这组数据的众数和中位数分别是( )
A、BC=3DE B、 = C、△ADE~△ABC D、S△ADE= S△ABC6. 甲、乙、丙三人站成一排拍照,则甲站在中间的概率是( )A、 B、 C、 D、7. 某校在国学文化进校园活动中,随机统计50名学生一周的课外阅读时间如表所示,这组数据的众数和中位数分别是( )学生数(人)
5
8
14
19
4
时间(小时)
6
7
8
9
10
A、14,9 B、9,9 C、9,8 D、8,98. 如图,是由几个完全相同的小正方体搭建的几何体,它的左视图是( )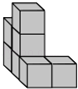 A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,反比例函数y= 的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为( )
9. 如图,反比例函数y= 的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为( )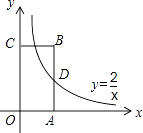 A、2 B、4 C、5 D、810. 如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1 , C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC= ,则AF的长度为( )
A、2 B、4 C、5 D、810. 如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1 , C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC= ,则AF的长度为( )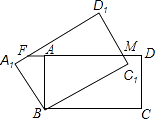 A、2﹣ B、 C、 D、 ﹣1
A、2﹣ B、 C、 D、 ﹣1二、填空题:
-
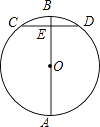
11. 计算:(﹣2ab)2= .12. 0.0000156用科学记数法表示为 .13. 分解因式:x3﹣4x= .14. 一个多边形的内角和为1080°,则这个多边形的边数是 .15. 函数y= 中,自变量x的取值范围为 .16. 如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径为 .
 17. 关于x的两个方程x2﹣x﹣6=0与 = 有一个解相同,则m= .18. 已知⊙O1和⊙O2的半径分别为m、n,且m、n满足 +(n﹣2)2=0,圆心距O1O2= ,则两圆的位置关系为 .19. 如图,小明购买一种笔记本所付款金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8个笔记本比分8次购买每次购买1个可节省元.
17. 关于x的两个方程x2﹣x﹣6=0与 = 有一个解相同,则m= .18. 已知⊙O1和⊙O2的半径分别为m、n,且m、n满足 +(n﹣2)2=0,圆心距O1O2= ,则两圆的位置关系为 .19. 如图,小明购买一种笔记本所付款金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8个笔记本比分8次购买每次购买1个可节省元.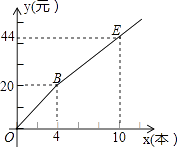 20. 阅读材料并解决问题:
20. 阅读材料并解决问题:求1+2+22+23+…+22014的值,令S=1+2+22+23+…+22014
等式两边同时乘以2,则2S=2+22+23+…+22014+22015
两式相减:得2S﹣S=22015﹣1
所以,S=22015﹣1
依据以上计算方法,计算1+3+32+33+…+32015= .
三、计算题
-
21.(1)、计算:|﹣ |﹣2cos45°﹣( )﹣1+(tan80°﹣ )0+(2)、化简:( ﹣2)÷ ﹣2x,再代入一个合适的x求值.
四、解答题
-
22. 如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD
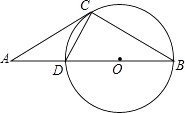 (1)、求证:AC是⊙O的切线;(2)、若⊙O的半径为2,求△ABC的面积.23. 2016年黔西南州教育局组织全州中小学生参加全省安全知识网络竞赛,在全州安全知识竞赛结束后,通过网上查询,某校一名班主任对本班成绩(成绩取整数,满分100分)作了统计分析,绘制成如下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
(1)、求证:AC是⊙O的切线;(2)、若⊙O的半径为2,求△ABC的面积.23. 2016年黔西南州教育局组织全州中小学生参加全省安全知识网络竞赛,在全州安全知识竞赛结束后,通过网上查询,某校一名班主任对本班成绩(成绩取整数,满分100分)作了统计分析,绘制成如下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题: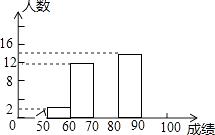 (1)、频数分布表中a= , b= , c=(2)、补全频数分布直方图(3)、为了激励学生增强安全意识,班主任准备从超过90分的学生中选2人介绍学习经验,那么取得100分的小亮和小华同时被选上的概率是多少?请用列表法或画树状图加以说明,并列出所有等可能结果.
(1)、频数分布表中a= , b= , c=(2)、补全频数分布直方图(3)、为了激励学生增强安全意识,班主任准备从超过90分的学生中选2人介绍学习经验,那么取得100分的小亮和小华同时被选上的概率是多少?请用列表法或画树状图加以说明,并列出所有等可能结果.频数分布表
分组(分)
频数
频率
50<x 60
2
0.04
60<x 70
12
a
70<x<80
b
0.36
80<x 90
14
0.28
90<x 100
c
0.08
合计
50
1
24. 我州某养殖场计划购买甲、乙两种鱼苗600条,甲种鱼苗每条16元,乙种鱼苗每条20元,相关资料表明:甲、乙两种鱼苗的成活率为80%,90%(1)、若购买这两种鱼苗共用去11000元,则甲、乙两种鱼苗各购买多少条?(2)、若要使这批鱼苗的总成活率不低于85%,则乙种鱼苗至少购买多少条?(3)、在(2)的条件下,应如何选购鱼苗,使购买鱼苗的总费用最低?最低费用是多少?25. 求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
 (1)、求108与45的最大公约数;(2)、求三个数78、104、143的最大公约数.26.
(1)、求108与45的最大公约数;(2)、求三个数78、104、143的最大公约数.26.如图,二次函数y=﹣x2+3x+m的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点
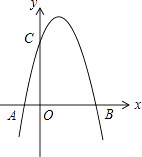 (1)、求m的值及C点坐标;(2)、在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由(3)、P为抛物线上一点,它关于直线BC的对称点为Q
(1)、求m的值及C点坐标;(2)、在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由(3)、P为抛物线上一点,它关于直线BC的对称点为Q①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.
-