2016年贵州省黔南州中考数学试卷
试卷更新日期:2016-11-02 类型:中考真卷
一、选择题
-
1. 一组数据:﹣5,﹣2,0,3,则该组数据中最大的数为( )A、﹣5 B、﹣2 C、0 D、32. 下面四个图形中,∠1=∠2一定成立的是( )A、
 B、
B、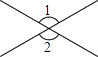 C、
C、 D、
D、 3. 如图是一个三棱柱笔筒,则该物体的主视图是( )
3. 如图是一个三棱柱笔筒,则该物体的主视图是( )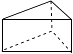 A、
A、 B、
B、 C、
C、 D、
D、 4. 一组数据:1,﹣1,3,x,4,它有唯一的众数是3,则这组数据的中位数为( )A、﹣1 B、1 C、3 D、45. 下列运算正确的是( )A、a3•a=a3 B、(﹣2a2)3=﹣6a5 C、a5+a5=a10 D、8a5b2÷2a3b=4a2b6. 下列说法中正确的是( )A、 化简后的结果是 B、9的平方根为3 C、 是最简二次根式 D、﹣27没有立方根7. 函数y= 的自变量x的取值范围在数轴上表示正确的是( )A、
4. 一组数据:1,﹣1,3,x,4,它有唯一的众数是3,则这组数据的中位数为( )A、﹣1 B、1 C、3 D、45. 下列运算正确的是( )A、a3•a=a3 B、(﹣2a2)3=﹣6a5 C、a5+a5=a10 D、8a5b2÷2a3b=4a2b6. 下列说法中正确的是( )A、 化简后的结果是 B、9的平方根为3 C、 是最简二次根式 D、﹣27没有立方根7. 函数y= 的自变量x的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 王杰同学在解决问题“已知A、B两点的坐标为A(3,﹣2)、B(6,﹣5)求直线AB关于x轴的对称直线A′B′的解析式”时,解法如下:先是建立平面直角坐标系(如图),标出A、B两点,并利用轴对称性质求出A′、B′的坐标分别为A′(3,2),B′(6,5);然后设直线A′B′的解析式为y=kx+b(k≠0),并将A′(3,2)、B′(6,5)代入y=kx+b中,得方程组 ,解得 ,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( )
8. 王杰同学在解决问题“已知A、B两点的坐标为A(3,﹣2)、B(6,﹣5)求直线AB关于x轴的对称直线A′B′的解析式”时,解法如下:先是建立平面直角坐标系(如图),标出A、B两点,并利用轴对称性质求出A′、B′的坐标分别为A′(3,2),B′(6,5);然后设直线A′B′的解析式为y=kx+b(k≠0),并将A′(3,2)、B′(6,5)代入y=kx+b中,得方程组 ,解得 ,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( ) A、分类讨论与转化思想 B、分类讨论与方程思想 C、数形结合与整体思想 D、数形结合与方程思想9. 如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y= (x<0)的图象经过顶点B,则k的值为( )
A、分类讨论与转化思想 B、分类讨论与方程思想 C、数形结合与整体思想 D、数形结合与方程思想9. 如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y= (x<0)的图象经过顶点B,则k的值为( ) A、﹣12 B、﹣27 C、﹣32 D、﹣3610. 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为( )
A、﹣12 B、﹣27 C、﹣32 D、﹣3610. 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O到弦CD的距离为( ) A、 cm B、3cm C、3 cm D、6cm11. y= x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0的根的情况为( )A、没有实数根 B、有一个实数根 C、有两个不相等的实数根 D、有两个相等的实数根12.
A、 cm B、3cm C、3 cm D、6cm11. y= x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0的根的情况为( )A、没有实数根 B、有一个实数根 C、有两个不相等的实数根 D、有两个相等的实数根12.如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
 A、
A、 B、
B、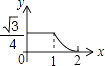 C、
C、 D、
D、 13. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a﹣b+c<0,其中正确的个数是( )
13. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a﹣b+c<0,其中正确的个数是( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
14. 若ab=2,a﹣b=﹣1,则代数式a2b﹣ab2的值等于 .15. 计算: +6(2016﹣π)0﹣( )﹣1+|﹣2|﹣cos30°= .16. 如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线ED交AB于点E,交BC于点D,若CD=3,则BD的长为 .
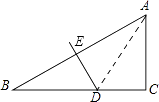 17. 如图,矩形ABCD的对角线AC的中点为O,过点O作OE⊥BC于点E,连接OD,已知AB=6,BC=8,则四边形OECD的周长为 .
17. 如图,矩形ABCD的对角线AC的中点为O,过点O作OE⊥BC于点E,连接OD,已知AB=6,BC=8,则四边形OECD的周长为 . 18. 在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
18. 在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:①△(a,b)=(﹣a,b);
②○(a,b)=(﹣a,﹣b);
③Ω(a,b)=(a,﹣b),
按照以上变换例如:△(○(1,2))=(1,﹣2),则○(Ω(3,4))等于 .
19. 为解决都匀市停车难的问题,计划在一段长为56米的路段规划处如图所示的停车位,已知每个车位是长为5米,宽为2米的矩形,且矩形的宽与路的边缘成45°角,则该路段最多可以划出个这样的停车位.(取 =1.4,结果保留整数)
三、解答题
-
20. 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上):
①把△ABC沿BA方向平移,请在网格中画出当点A移动到点A1时的△A1B1C1;
②把△A1B1C1绕点A1按逆时针方向旋转90°后得到△A2B2C2 , 如果网格中小正方形的边长为1,求点B1旋转到B2的路径长.
 21. 解方程: .22. “2016国际大数据产业博览会”于5月25日至5月29日在贵阳举行.参展内容为:A﹣经济和社会发展;B﹣产业与应用;C﹣技术与趋势;D﹣安全和隐私保护;E﹣电子商务,共五大板块,为了解观众对五大板块的“关注情况”,某机构进行了随机问卷调查,并将调查结果绘制成如下两幅统计图(均不完整),请根据统计图中提供的信息,解答下列问题:
21. 解方程: .22. “2016国际大数据产业博览会”于5月25日至5月29日在贵阳举行.参展内容为:A﹣经济和社会发展;B﹣产业与应用;C﹣技术与趋势;D﹣安全和隐私保护;E﹣电子商务,共五大板块,为了解观众对五大板块的“关注情况”,某机构进行了随机问卷调查,并将调查结果绘制成如下两幅统计图(均不完整),请根据统计图中提供的信息,解答下列问题: (1)、本次随机调查了多少名观众?(2)、请补全统计图,并求出扇形统计图中“D﹣安全和隐私保护”所对应的扇形圆心角的度数.(3)、据相关报道,本次博览会共吸引力90000名观众前来参观,请估计关注“E﹣电子商务”的人数是多少?23. 为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.(1)、小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?(2)、小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或;列表的方法进行说明.24. 已知二次函数y=x2+bx+c的图象与y轴交于点C(0,﹣6),与x轴的一个交点坐标是A(﹣2,0).
(1)、本次随机调查了多少名观众?(2)、请补全统计图,并求出扇形统计图中“D﹣安全和隐私保护”所对应的扇形圆心角的度数.(3)、据相关报道,本次博览会共吸引力90000名观众前来参观,请估计关注“E﹣电子商务”的人数是多少?23. 为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.(1)、小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?(2)、小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或;列表的方法进行说明.24. 已知二次函数y=x2+bx+c的图象与y轴交于点C(0,﹣6),与x轴的一个交点坐标是A(﹣2,0). (1)、求二次函数的解析式,并写出顶点D的坐标;(2)、将二次函数的图象沿x轴向左平移 个单位长度,当 y<0时,求x的取值范围.25. 如图,AB是⊙O的直径,点D是 上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)、求二次函数的解析式,并写出顶点D的坐标;(2)、将二次函数的图象沿x轴向左平移 个单位长度,当 y<0时,求x的取值范围.25. 如图,AB是⊙O的直径,点D是 上一点,且∠BDE=∠CBE,BD与AE交于点F. (1)、求证:BC是⊙O的切线;(2)、若BD平分∠ABE,求证:DE2=DF•DB;(3)、在(2)的条件下,延长ED、BA交于点P,若PA=AO,DE=2,求PD的长.26. 都匀某校准备组织学生及家长代表到桂林进行社会实践活动,为便于管理,所有人员必须乘坐同一列高铁,高铁单程票价格如表所示,二等座学生票可打7.5折,已知所有人员都买一等座单程火车票需6175元,都买二等座单程火车票需3150元;如果家长代表与教师的人数之比为2:1.
(1)、求证:BC是⊙O的切线;(2)、若BD平分∠ABE,求证:DE2=DF•DB;(3)、在(2)的条件下,延长ED、BA交于点P,若PA=AO,DE=2,求PD的长.26. 都匀某校准备组织学生及家长代表到桂林进行社会实践活动,为便于管理,所有人员必须乘坐同一列高铁,高铁单程票价格如表所示,二等座学生票可打7.5折,已知所有人员都买一等座单程火车票需6175元,都买二等座单程火车票需3150元;如果家长代表与教师的人数之比为2:1.运行区间
票价
起点站
终点站
一等座
二等座
都匀
桂林
95(元)
60(元)
(1)、参加社会实践活动的老师、家长代表与学生各有多少人?(2)、由于各种原因,二等座单程火车票只能买x张(x<参加社会实践的总人数),其余的须买一等座单程火车票,在保证所有人员都有座位的前提下,请你设计最经济的购票方案,并写出购买单程火车票的总费用y与x之间的函数关系式.(3)、在(2)的方案下,请求出当x=30时,购买单程火车票的总费用.27.如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥AO,交BO于点N,连结ND、BM,设OP=t.
 (1)、求点M的坐标(用含t的代数式表示);(2)、试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由.(3)、当t为何值时,四边形BNDM的面积最小;(4)、在x轴正半轴上存在点Q,使得△QMN是等腰三角形,请直接写出不少于4个符合条件的点Q的坐标(用含t的式子表示).
(1)、求点M的坐标(用含t的代数式表示);(2)、试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由.(3)、当t为何值时,四边形BNDM的面积最小;(4)、在x轴正半轴上存在点Q,使得△QMN是等腰三角形,请直接写出不少于4个符合条件的点Q的坐标(用含t的式子表示).