2016年广西梧州市中考数学试卷

试卷更新日期：2016-11-02 类型：中考真卷

进入出卷网下载

一、选择题

1. $\frac{1}{6}$ 的倒数是（）

A、﹣ $\frac{1}{6}$ B、 $\frac{1}{6}$ C、﹣6 D、6

查看试题解析
2. 下列“禁止行人通行，注意危险，禁止非机动车通行，限速60”四个交通标志图中，为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若式子 $\sqrt{m}$ ﹣3有意义，则m的取值范围是（）

A、m≥3 B、m≤3 C、m≥0 D、m≤0

查看试题解析
4. 一元一次方程3x﹣3=0的解是（）

A、x=1 B、x=﹣1 C、x= $\frac{1}{3}$ D、x=0

查看试题解析
5. 分解因式：2x²﹣2=（）

A、2（x²﹣1） B、2（x²+1） C、2（x﹣1）² D、2（x+1）（x﹣1）

查看试题解析
6. 已知半径为5的圆，其圆心到直线的距离是3，此时直线和圆的位置关系为（）

A、相离 B、相切 C、相交 D、无法确定

查看试题解析
7. 在△ABC中，AB=3，BC=4，AC=2，D、E、F分别为AB、BC、AC中点，连接DF、FE，则四边形DBEF的周长是（）

A、5 B、7 C、9 D、11

查看试题解析
8. 下列命题：
①对顶角相等；
②同位角相等，两直线平行；
③若a=b，则|a|=|b|；
④若x=0，则x²﹣2x=0
它们的逆命题一定成立的有（）

A、①②③④ B、①④ C、②④ D、②

查看试题解析
9. 三张背面完全相同的数字牌，它们的正面分别印有数字“1”、“2”、“3”，将它们背面朝上，洗匀后随机抽取一张，记录牌上的数字并把牌放回，再重复这样的步骤两次，得到三个数字a、b、c，则以a、b、c为边长正好构成等边三角形的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{27}$ C、 $\frac{5}{9}$ D、 $\frac{1}{3}$

查看试题解析
10. 青山村种的水稻2010年平均每公顷产7200kg，2012年平均每公顷产8450kg，求水稻每公顷产量的年平均增长率，设水稻每公顷产量的年平均增长率为x，则所列方程正确的为（）

A、7200（1+x）=8450 B、7200（1+x）²=8450 C、7200+x²=8450 D、8450（1﹣x）²=7200

查看试题解析
11. 在平面直角坐标系中，直线y=x+b与双曲线y=﹣ $\frac{1}{x}$ 只有一个公共点，则b的值是（）

A、1 B、±1 C、±2 D、2

查看试题解析
12.
如图所示，抛物线y=ax²+bx+c（a≠0）与x轴交于点A（﹣2，0）、B（1，0），直线x=﹣0.5与此抛物线交于点C，与x轴交于点M，在直线上取点D，使MD=MC，连接AC、BC、AD、BD，某同学根据图象写出下列结论：
①a﹣b=0；
②当﹣2＜x＜1时，y＞0；
③四边形ACBD是菱形；
④9a﹣3b+c＞0
你认为其中正确的是（）

A、②③④ B、①②④ C、①③④ D、①②③

查看试题解析

二、填空题

13. 计算：3a﹣2a= ．

查看试题解析
14. 2016年1月，梧州市西江特大桥完成桥墩水下桩基础，累计完成投资53 000 000元，其中53 000 000用科学记数法表示为．

查看试题解析
15. 点P（2，﹣3）先向左平移4个单位长度，再向上平移1个单位长度，得到点P′的坐标是．

查看试题解析
16. 若一个正多边形的一个外角等于18°，则这个正多边形的边数是．

查看试题解析
17. 如图，点B、C把 $\hat{A D}$ 分成三等分，ED是⊙O的切线，过点B、C分别作半径的垂线段，已知∠E=45°，半径OD=1，则图中阴影部分的面积是．

查看试题解析
18. 如图，在坐标轴上取点A₁（2，0），作x轴的垂线与直线y=2x交于点B₁ ，作等腰直角三角形A₁B₁A₂；又过点A₂作x轴的垂线交直线y=2x交于点B₂ ，作等腰直角三角形A₂B₂A₃；…，如此反复作等腰直角三角形，当作到A_n（n为正整数）点时，则A_n的坐标是．

查看试题解析

三、解答题

19. 计算：|﹣3|﹣（﹣2016）⁰+（﹣2）×（﹣3）+tan45°．

查看试题解析
20. 解不等式组 ${\begin{matrix} 2 (1 - x) + 3 > 0 ① \\ x + 2 \geq 1 ② \end{matrix}$ ，并在数轴上表示不等式组的解集．

查看试题解析
21.
在“立德树人，志愿服务”活动月中，学校团委为了解本校学生一个月内参加志愿服务次数的情况，随机抽取了部分同学进行统计，并将统计结果分别分成A、B、C、D四类，根据统计结果绘制了如图所示的两幅不完整的统计图．
请根据图中信息解答下列问题：

(1)、本次抽样调查了名学生，并请补全条形统计图；

(2)、被调查学生“一个月内参加志愿服务次数”的人数的众数落在类．

查看试题解析
22. 如图，过⊙O上的两点A、B分别作切线，并交BO、AO的延长线于点C、D，连接CD，交⊙O于点E、F，过圆心O作OM⊥CD，垂足为M点．求证：

(1)、△ACO≌△BDO；

(2)、CE=DF．

查看试题解析
23. 如图，四边形ABCD是一片水田，某村民小组需计算其面积，测得如下数据：
∠A=90°，∠ABD=60°，∠CBD=54°，AB=200m，BC=300m．
请你计算出这片水田的面积．
（参考数据：sin54°≈0.809，cos54°≈0.588，tan54°≈1.376， $\sqrt{3}$ ≈1.732）

查看试题解析
24. 为了提高身体素质，有些人选择到专业的健身中心锻炼身体，某健身中心的消费方式如下：
普通消费：35元/次；
白金卡消费：购卡280元/张，凭卡免费消费10次再送2次；
钻石卡消费：购卡560元/张，凭卡每次消费不再收费．
以上消费卡使用年限均为一年，每位顾客只能购买一张卡，且只限本人使用．

(1)、李叔叔每年去该健身中心健身6次，他应选择哪种消费方式更合算？

(2)、设一年内去该健身中心健身x次（x为正整数），所需总费用为y元，请分别写出选择普通消费和白金卡消费的y与x的函数关系式；

(3)、王阿姨每年去该健身中心健身至少18次，请通过计算帮助王阿姨选择最合算的消费方式．

查看试题解析
25. 在矩形ABCD中，E为CD的中点，H为BE上的一点， $\frac{E H}{B H} = 3$ ，连接CH并延长交AB于点G，连接GE并延长交AD的延长线于点F．

(1)、求证： $\frac{E C}{B G} = \frac{E H}{B H}$ ；

(2)、若∠CGF=90°，求 $\frac{A B}{B C}$ 的值．

查看试题解析
26.
如图，抛物线y=ax²+bx﹣4（a≠0）与x轴交于A（4，0）、B（﹣1，0）两点，过点A的直线y=﹣x+4交抛物线于点C．

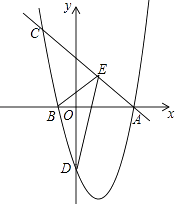(1)、求此抛物线的解析式；

(2)、在直线AC上有一动点E，当点E在某个位置时，使△BDE的周长最小，求此时E点坐标；

(3)、当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时，是否存在使△BDE为直角三角形的情况，若存在，请直接写出符合要求的E点的坐标；若不存在，请说明理由．

查看试题解析