2016年广西来宾市中考数学试卷

试卷更新日期：2016-11-02 类型：中考真卷

进入出卷网下载

一、选择题

1. 下列计算正确的是（）

A、x²+x²=x⁴ B、x²+x³=2x⁵ C、3x﹣2x=1 D、x²y﹣2x²y=﹣x²y

查看试题解析
2. 如图，在下列条件中，不能判定直线a与b平行的是（）

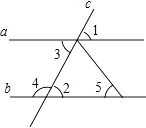A、∠1=∠2 B、∠2=∠3 C、∠3=∠5 D、∠3+∠4=180°

查看试题解析
3. 计算（﹣ $\frac{1}{2}$ ）⁰﹣ $\sqrt{4}$ =（）

A、﹣1 B、﹣ $\frac{3}{2}$ C、﹣2 D、﹣ $\frac{5}{2}$

查看试题解析
4. 如果一个正多边形的一个外角为30°，那么这个正多边形的边数是（）

A、6 B、11 C、12 D、18

查看试题解析
5. 下列计算正确的是（）

A、（﹣x³）²=x⁵ B、（﹣3x²）²=6x⁴ C、（﹣x）^﹣²= $\frac{1}{x^{2}}$ D、x⁸÷x⁴=x²

查看试题解析
6. 已知x₁、x₂是方程x²+3x﹣1=0的两个实数根，那么下列结论正确的是（）

A、x₁+x₂=﹣1 B、x₁+x₂=﹣3 C、x₁+x₂=1 D、x₁+x₂=3

查看试题解析
7. 计算（2x﹣1）（1﹣2x）结果正确的是（）

A、4x²﹣1 B、1﹣4x² C、﹣4x²+4x﹣1 D、4x²﹣4x+1

查看试题解析
8. 下列计算正确的是（）

A、 $\sqrt{5}$ ﹣ $\sqrt{3}$ = $\sqrt{2}$ B、3 $\sqrt{5}$ ×2 $\sqrt{3}$ =6 $\sqrt{15}$ C、（2 $\sqrt{2}$ ）²=16 D、 $\frac{3}{\sqrt{3}}$ =1

查看试题解析
9. 如图，在△ABC中，AB=4，BC=6，DE、DF是△ABC的中位线，则四边形BEDF的周长是（）

A、5 B、7 C、8 D、10

查看试题解析
10. 一种饮料有两种包装，5大盒、4小盒共装148瓶，2大盒、5小盒共装100瓶，大盒与小盒每盒各装多少瓶？设大盒装x瓶，小盒装y瓶，则可列方程组（）

A、 ${\begin{matrix} 5 x + 4 y = 148 \\ 2 x + 5 y = 100 \end{matrix}$ B、 ${\begin{matrix} 4 x + 5 y = 148 \\ 2 x + 5 y = 100 \end{matrix}$ C、 ${\begin{matrix} 5 x + 4 y = 148 \\ 5 x + 2 y = 100 \end{matrix}$ D、 ${\begin{matrix} 4 x + 5 y = 148 \\ 5 x + 2 y = 100 \end{matrix}$

查看试题解析
11. 下列3个图形中，能通过旋转得到右侧图形的有（）

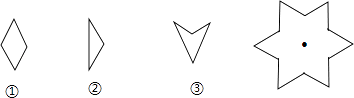A、①② B、①③ C、②③ D、①②③

查看试题解析
12. 当x=6，y=﹣2时，代数式 $\frac{x^{2} - y^{2}}{{(x - y)}^{2}}$ 的值为（）

A、2 B、 $\frac{4}{3}$ C、1 D、 $\frac{1}{2}$

查看试题解析
13. 设抛物线C₁：y=x²向右平移2个单位长度，再向下平移3个单位长度得到抛物线C₂ ，则抛物线C₂对应的函数解析式是（）

A、y=（x﹣2）²﹣3 B、y=（x+2）²﹣3 C、y=（x﹣2）²+3 D、y=（x+2）²+3

查看试题解析
14. 已知直线l₁：y=﹣3x+b与直线l₂：y=﹣kx+1在同一坐标系中的图象交于点（1，﹣2），那么方程组 ${\begin{matrix} 3 x + y = b \\ k x + y = 1 \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 1 \\ y = - 2 \end{matrix}$ B、 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ C、 ${\begin{matrix} x = - 1 \\ y = - 2 \end{matrix}$ D、 ${\begin{matrix} x = - 1 \\ y = 2 \end{matrix}$

查看试题解析
15. 已知不等式组 ${\begin{matrix} x > a \\ x \geq 1 \end{matrix}$ 的解集是x≥1，则a的取值范围是（）

A、a＜1 B、a≤1 C、a≥1 D、a＞1

查看试题解析

二、填空题

16. 将数字185000用科学记数法表示为．

查看试题解析
17. 计算：|1﹣3|= ．

查看试题解析
18. 如图，在⊙O中，点A、B、C在⊙O上，且∠ACB=110°，则∠α= ．

查看试题解析
19. 已知函数y=﹣x²﹣2x，当时，函数值y随x的增大而增大．

查看试题解析
20. 命题“直径所对的圆周角是直角”的逆命题是．

查看试题解析

三、解答题

21. 甲、乙两名射击运动员在某次训练中各射击10发子弹，成绩如表：
甲
8
9
7
9
8
6
7
8
10
8
乙
6
7
9
7
9
10
8
7
7
10
且 $\bar{x_{乙}}$ =8，S_乙²=1.8，根据上述信息完成下列问题：

(1)、将甲运动员的折线统计图补充完整；

(2)、乙运动员射击训练成绩的众数是，中位数是．

(3)、求甲运动员射击成绩的平均数和方差，并判断甲、乙两人本次射击成绩的稳定性．

查看试题解析
22. 已知反比例函数y= $\frac{k}{x}$ 与一次函数y=x+2的图象交于点A（﹣3，m）

(1)、求反比例函数的解析式；

(2)、如果点M的横、纵坐标都是不大于3的正整数，求点M在反比例函数图象上的概率．

查看试题解析
23. 如图，在正方形ABCD中，点E（与点B、C不重合）是BC边上一点，将线段EA绕点E顺时针旋转90°到EF，过点F作BC的垂线交BC的延长线于点G，连接CF．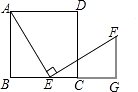

(1)、求证：△ABE≌△EGF；

(2)、若AB=2，S_△_ABE=2S_△_ECF ，求BE．

查看试题解析
24. 某商场第一次用11000元购进某款拼装机器人进行销售，很快销售一空，商家又用24000元第二次购进同款机器人，所购进数量是第一次的2倍，但单价贵了10元．

(1)、求该商家第一次购进机器人多少个？

(2)、若所有机器人都按相同的标价销售，要求全部销售完毕的利润率不低于20%（不考虑其它因素），那么每个机器人的标价至少是多少元？

查看试题解析
25. 如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，DE⊥AD，交AB于点E，AE为⊙O的直径

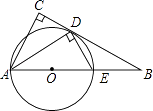(1)、判断BC与⊙O的位置关系，并证明你的结论；

(2)、求证：△ABD∽△DBE；

(3)、若cosB= $\frac{2 \sqrt{2}}{3}$ ，AE=4，求CD．

查看试题解析
26.
如图，在矩形ABCD中，AB=10，AD=6，点M为AB上的一动点，将矩形ABCD沿某一直线对折，使点C与点M重合，该直线与AB（或BC）、CD（或DA）分别交于点P、Q

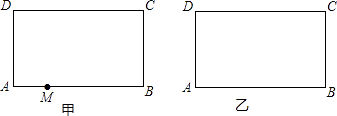(1)、用直尺和圆规在图甲中画出折痕所在直线（不要求写画法，但要求保留作图痕迹）

(2)、如果PQ与AB、CD都相交，试判断△MPQ的形状并证明你的结论；

(3)、设AM=x，d为点M到直线PQ的距离，y=d² ，
①求y关于x的函数解析式，并指出x的取值范围；
②当直线PQ恰好通过点D时，求点M到直线PQ的距离．

查看试题解析

甲	8	9	7	9	8	6	7	8	10	8
乙	6	7	9	7	9	10	8	7	7	10