2016年福建省泉州市中考数学试卷

试卷更新日期：2016-11-02 类型：中考真卷

进入 出卷网 下载

一、选择题：每小题四个答案，其中有且只有一个答案是正确的，请在答题卡上相应题目的答题区域内作答．

  • 1. ﹣3的绝对值是（  ）
    A、3 B、﹣3 C、﹣ 13 D、13

    查看试题解析

  • 2. （x2y）3的结果是（  ）
    A、x5y3 B、x6y C、3x2y D、x6y3

    查看试题解析

  • 3. 不等式组 {x−1>0x≤2 的解集是（  ）
    A、x≤2 B、x＞1 C、1＜x≤2 D、无解

    查看试题解析

  • 4. 如图，AB和⊙O相切于点B，∠AOB=60°，则∠A的大小为（  ）

    A、15° B、30° C、45° D、60°

    查看试题解析

  • 5. 一组数据：2，5，4，3，2的中位数是（  ）

    A、4 B、3.2 C、3 D、2

    查看试题解析

  • 6. 如图，圆锥底面半径为rcm，母线长为10cm，其侧面展开图是圆心角为216°的扇形，则r的值为（  ）

    A、3 B、6 C、3π D、6π

    查看试题解析

  • 7. 如图，已知点A（﹣8，0），B（2，0），点C在直线y=﹣ 34x+4 上，则使△ABC是直角三角形的点C的个数为（  ）

    A、1 B、2 C、3 D、4

    查看试题解析

二、填空题：在答题卡上相应题目的答题区域内作答．

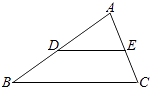
  • 8. 27的立方根为 ．

    查看试题解析

  • 9. 中国的陆地面积约为9 600 000km2 ， 把9 600 000用科学记数法表示为 ．

    查看试题解析

  • 10. 因式分解：1﹣x2= ．

    查看试题解析

  • 11. 如图，在△ABC中，D、E分别是边AB、AC的中点，BC=8，则DE= ．

    查看试题解析

  • 12. 十边形的外角和是 ．

    查看试题解析

  • 13. 计算： 3mm+1+3m+1 = ．

    查看试题解析

  • 14. 如图，在Rt△ABC中，E是斜边AB的中点，若AB=10，则CE= ．

    查看试题解析

  • 15.

    如图，⊙O的弦AB、CD相交于点E，若CE：BE=2：3，则AE：DE=

    查看试题解析

  • 16.

    找出下列各图形中数的规律，依此，a的值为 ．

    查看试题解析

  • 17.

    如图，在四边形ABCD中，AB∥DC，E是AD中点，EF⊥BC于点F，BC=5，EF=3．


    (1)、若AB=DC，则四边形ABCD的面积S=；

    (2)、若AB＞DC，则此时四边形ABCD的面积S′ S（用“＞”或“=”或“＜”填空）．

    查看试题解析

三、解答题：在答题卡相应题目的答题区域内作答．

  • 18. 计算：（π﹣3）0+|﹣2|﹣ 20 ÷ 5 +（﹣1）﹣1 ．

    查看试题解析

  • 19. 先化简，再求值：（x+2）2﹣4x（x+1），其中x= 2 ．

    查看试题解析

  • 20. 如图，△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°，点E在AB上．求证：△CDA≌△CEB．

    查看试题解析

  • 21. A、B两组卡片共5张，A中三张分别写有数字2，4，6，B中两张分别写有3，5，它们除数字外没有任何区别．
    (1)、随机地从A中抽取一张，求抽到数字为2的概率；
    (2)、随机地分别从A、B中各抽取一张，请你用画树状图或列表的方法表示所有等可能的结果．现制定这样一个游戏规则：若所选出的两数之积为3的倍数，则甲获胜；否则乙获胜．请问这样的游戏规则对甲乙双方公平吗？为什么？

    查看试题解析

  • 22. 近期，我市中小学广泛开展了“传承中华文化，共筑精神家园”爱国主义读书教育活动，某中学为了解学生最喜爱的活动形式，以“我最喜爱的一种活动”为主题，进行随机抽样调查，收集数据整理后，绘制出以下两幅不完整的统计图表，请根据图中提供的信息，解答下面的问题：

    最喜爱的一种活动统计表

    活动形式

    征文

    讲故事

    演讲

    网上竞答

    其他

    人数

    60

    30

    39

    a

    b

    (1)、在这次抽样调查中，一共调查了多少名学生？扇形统计图中“讲故事”部分的圆心角是多少度？
    (2)、如果这所中学共有学生3800名，那么请你估计最喜爱征文活动的学生人数．

    查看试题解析

  • 23. 已知反比例函数的图象经过点P（2，﹣3）．
    (1)、求该函数的解析式；
    (2)、若将点P沿x轴负方向平移3个单位，再沿y轴方向平移n（n＞0）个单位得到点P′，使点P′恰好在该函数的图象上，求n的值和点P沿y轴平移的方向．

    查看试题解析

  • 24. 某进口专营店销售一种“特产”，其成本价是20元/千克，根据以往的销售情况描出销量y（千克/天）与售价x（元/千克）的关系，如图所示．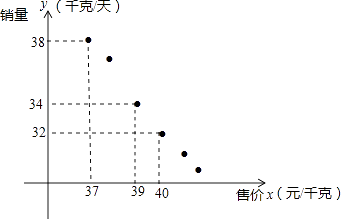

    (1)、试求出y与x之间的一个函数关系式；
    (2)、利用（1）的结论：

    求每千克售价为多少元时，每天可以获得最大的销售利润．

     ②进口产品检验、运输等过程需耗时5天，该“特产”最长的保存期为一个月（30天），若售价不低于30元/千克，则一次进货最多只能多少千克？

    查看试题解析

  • 25. 我们知道：垂直于弦的直径平分这条弦，并且平分这条弦所对的两条弧；平分弧的直径垂直平分这条弧所对的弦．你可以利用这一结论解决问题：

    如图，点P在以MN（南北方向）为直径的⊙O上，MN=8，PQ⊥MN交⊙O于点Q，垂足为H，PQ≠MN，弦PC、PD分别交MN于点E、F，且PE=PF．

    (1)、比较 CQ^ 与 DQ^ 的大小；
    (2)、若OH=2 2 ，求证：OP∥CD；
    (3)、设直线MN、CD相交所成的锐角为α，试确定cosα= 32 时，点P的位置．

    查看试题解析

  • 26. 如图，在四边形ABCD中，AD∥BC，∠A=∠C，点P在边AB上．

    (1)、判断四边形ABCD的形状并加以证明；
    (2)、若AB=AD，以过点P的直线为轴，将四边形ABCD折叠，使点B、C分别落在点B′、C′上，且B′C′经过点D，折痕与四边形的另一交点为Q．

    ①在图2中作出四边形PB′C′Q（保留作图痕迹，不必说明作法和理由）；

    ②如果∠C=60°，那么 APPB 为何值时，B′P⊥AB．

    查看试题解析