江苏省南通市启东市2015-2016学年八年级下册数学开学考试试卷

试卷更新日期：2018-01-23 类型：开学考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（　　）

A、2a²+a=3a³ B、（﹣a）²÷a=a C、（﹣a）³•a²=﹣a⁶ D、（2a²）³=6a⁶

查看试题解析
2. 在 $\frac{1}{x}$ , $\frac{1}{2}$ , $\frac{x^{2} + 1}{2}$ , $\frac{3 x y}{π}$ , $\frac{3}{x + y}$ ,a+ $\frac{1}{m}$ 中，分式的个数是（　　）

A、2 B、3 C、4 D、5

查看试题解析
3.
如图，在△ABC和△BDE中，点C在边BD上，边AC交边BE于点F．若AC=BD，AB=ED，BC=BE，则∠ACB等于（　　）

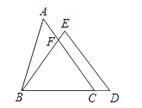A、∠EDB B、∠BED C、 $\frac{1}{2}$ ∠AFB D、2∠ABF

查看试题解析
4. 已知：如图，AC=CD，∠B=∠E=90°，AC⊥CD，则不正确的结论是（）

A、∠A与∠D互为余角 B、∠A=∠2 C、△ABC≌△CED D、∠1=∠2

查看试题解析
5.
如图，锐角三角形ABC中，直线L为BC的中垂线，直线M为∠ABC的角平分线，L与M相交于P点．若∠A=60°，∠ACP=24°，则∠ABP的度数为何？（　　）

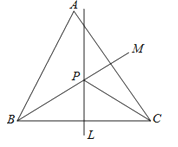A、24° B、30° C、32° D、36°

查看试题解析
6. 使分式 $\frac{x - 2}{(x - 1) (x - 2)}$ 有意义，x应满足的条件是（）

A、x≠1 B、x≠2 C、x≠1或x≠2 D、x≠1且x≠2

查看试题解析
7. 下列各式：①x²﹣10x+25；②x²﹣2x﹣1；③4a²﹣4a﹣1；④﹣m²+m﹣ $\frac{1}{4}$ ；⑤4x²﹣x²+ $\frac{1}{4}$ ．其中不能用完全平方公式分解的个数为（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8.
把一张形状是矩形的纸片剪去其中某一个角，剩下的部分是一个多边形，则这个多边形的内角和不可能是（　　）

A、720° B、540° C、360° D、180°

查看试题解析
9.
如图，∠AOB=30°，∠AOB内有一定点P，且OP=10．在OA上有一点Q，OB上有一点R．若△PQR周长最小，则最小周长是（　　）

A、10 B、15 C、20 D、30

查看试题解析
10. 甲、乙两地之间的高速公路全长200千米，比原来国道的长度减少了20千米．高速公路通车后，某长途汽车的行驶速度提高了45千米/时，从甲地到乙地的行驶时间缩短了一半．设该长途汽车在原来国道上行驶的速度为x千米/时，根据题意，下列方程正确的是（）

A、 $\frac{200}{x} = \frac{180}{x - 45} \cdot \frac{1}{2}$ B、 $\frac{200}{x} = \frac{220}{x - 45} \cdot \frac{1}{2}$ C、 $\frac{200}{x + 45} = \frac{180}{x} \cdot \frac{1}{2}$ D、 $\frac{200}{x + 45} = \frac{220}{x} \cdot \frac{1}{2}$

查看试题解析

二、填空题

11. 分解因式：a³﹣9a= ．

查看试题解析
12. 若点A（m+2，3）与点B（﹣4，n+5）关于y轴对称，则m+n=

查看试题解析
13.
如图，在△ABC中，∠C=90°，AB=10，AD是△ABC的一条角平分线．若CD=3，则△ABD的面积为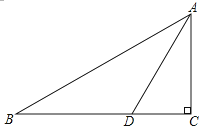

查看试题解析
14. 如图，在△ABC中，AB=AC，点O在△ABC内，且∠OBC=∠OCA，∠BOC=110°，求∠A的度数= ．

查看试题解析
15. 若分式方程： $2 + \frac{1 - k x}{x - 2} = \frac{1}{2 - x}$ 有增根，则k= ．

查看试题解析
16.
将正三角形、正四边形、正五边形按如图所示的位置摆放．如果∠3=32°，那么∠1+∠2= 度．

查看试题解析
17. 甲、乙两种糖果的单价分别为20元/千克和24元/千克，将两种糖果按一定的比例混合销售．在两种糖果混合比例保持不变的情况下，将甲种糖果的售价上涨8%，乙种糖果的售价下跌10%，使调整前后混合糖果的单价保持不变，则两种糖果的混合比例应为：甲：乙=

查看试题解析
18. 如图，坐标平面上，△ABC≌△DEF全等，其中A、B、C的对应顶点分别为D、E、F，且AB=BC，若A、B、C的坐标分别为（﹣3，1）、（﹣6，﹣3）、（﹣1，﹣3），D、E两点在y轴上，则F点到y轴的距离为．

查看试题解析

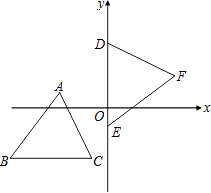
三、解答题

19. 用乘法公式计算,利用公式计算

(1)、998×1002；

(2)、（3a+2b﹣1）（3a﹣2b+1）

查看试题解析
20.

(1)、因式分解：a（n﹣1）²﹣2a（n﹣1）+a．

(2)、解方程： $\frac{x}{x + 1} - 1 = \frac{2 x}{3 x + 3}$ ．

查看试题解析
21. 先化简，再求值：（ $\frac{3 x}{x - 2}$ ﹣ $\frac{x}{x + 2}$ ）÷ $\frac{x}{x^{2} - 4}$ ，在﹣2，0，1，2四个数中选一个合适的代入求值．

查看试题解析
22.
如图，点C，F在线段BE上，BF=EC，∠1=∠2，请你添加一个条件，使△ABC≌△DEF，并加以证明．（不再添加辅助线和字母）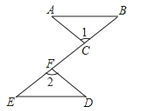

查看试题解析
23.
如图，树AB垂直于地面，为测树高，小明在C处，测得∠ACB=15°，他沿CB方向走了20米，到达D处，测得∠ADB=30°，你能帮助小明计算出树的高度吗？

查看试题解析
24. 如图所示，在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形．

(1)、用a，b，x表示纸片剩余部分的面积；

(2)、当a=6，b=4，且剪去部分的面积等于剩余部分的面积时，求正方形的边长．

查看试题解析
25. 作图题：（要求保留作图痕迹，不写作法）

(1)、作△ABC中BC边上的垂直平分线EF（交AC于点E，交BC于点F）；

(2)、连结BE，若AC=10，AB=6，求△ABE的周长．

查看试题解析
26. 如图，已知在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．试探索BF与CF的数量关系，写出你的结论并证明．

查看试题解析
27. 荣庆公司计划从商店购买同一品牌的台灯和手电筒，已知购买一个台灯比购买一个手电筒多用20元，若用400元购买台灯和用160元购买手电筒，则购买台灯的个数是购买手电筒个数的一半．

(1)、求购买该品牌一个台灯、一个手电筒各需要多少元？

(2)、经商谈，商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠，如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个，且该公司购买台灯和手电筒的总费用不超过670元，那么荣庆公司最多可购买多少个该品牌台灯？

查看试题解析
28. 在△ABC中，AB=AC，∠BAC=α（0°＜α＜60°），分别以AB、BC为边作等边三角形ABE和等边三角形BCD，连结CE，如图1所示．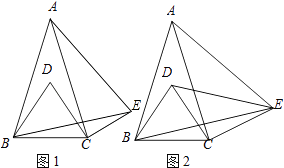

(1)、直接写出∠ABD的大小（用含α的式子表示）；

(2)、判断DC与CE的位置关系，并加以证明；

(3)、在（2）的条件下，连结DE，如图2，若∠DEC=45°，求α的值．

查看试题解析