江苏省东台市民办校联盟2016-2017学年八年级下册数学开学考试试卷
试卷更新日期:2018-01-23 类型:开学考试
一、单选题
-
1. 下列四个数中,最小的数是( )A、1 B、0 C、 D、2. 为了了解我市2017年中考数学学科各分数段成绩分布情况,从中抽取150名考生的中考数学成绩进行统计分析.在这个问题中,样本是指( )A、150 B、被抽取的150名考生 C、被抽取的150名考生的中考数学成绩 D、我市2013年中考数学成绩3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、正三角形 B、正方形 C、等腰三角形 D、平行四边形4. 在平面直角坐标系中,点P(1,-3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 在反比例函数y= 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( ).
A、k>1 B、k>0 C、k≥1 D、k<16. 下列说法中的错误的是( )A、一组邻边相等的矩形是正方形 B、一组邻边相等的平行四边形是菱形 C、一组对边相等且有一个角是直角的四边形是矩形 D、一组对边平行且相等的四边形是平行四边形7. 如图,在▱ABCD中,∠ODA= 90°,AC=10 cm,BD=6 cm,则BC的长为( )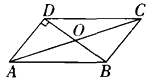 A、4 cm B、5 cm C、6 cm D、8 cm8. 已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )A、
A、4 cm B、5 cm C、6 cm D、8 cm8. 已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )A、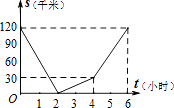 B、
B、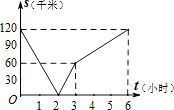 C、
C、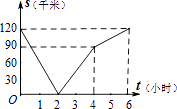 D、
D、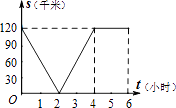
二、填空题
-
9. 若分式 在实数范围内有意义,则x的取值范围是 .10. 计算 的结果是 .11. 在一个不透明的袋子中有10个除颜色外其余均相同的小球,通过多次摸球实验后,发现摸到白球的频率约为40%,估计袋子中白球有个。12. 一个反比例函数y= (k≠0)的图象经过点P(-2,-3),则该反比例函数的解析式是 .13. 已知x=3是关于x的方程 的一个根,则
14. 若 ,则 =15. 若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则k的取值范围是16. 若分式方程 有增根,则m的值是17. 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是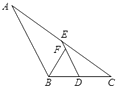 18. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数 (x<0)图象上一点,AO的延长线交函数 (x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于
18. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数 (x<0)图象上一点,AO的延长线交函数 (x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于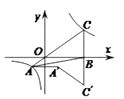
三、解答题
-
19. 计算题化简及求值
(1)、计算题(2)、化简
20. 解方程:分式方程和一元二次方程
(1)、(2)、x(x-2)=3x-621. 化简、求值: .22. 随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30﹣40含起点值30,不含终点值40),得到其频数及频率如表: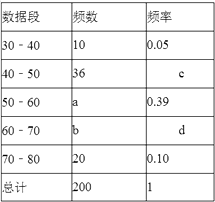
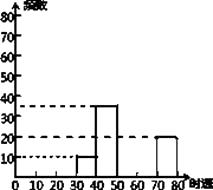 (1)、表中a、b、c、d分别为:a=; b=; c=; d=.(2)、补全频数分布直方图;(3)、如果某天该路段约有1500辆通过,汽车时速不低于60千米即为违章,通过该统计数据估计当天违章车辆约有多少辆?23. 如图,E、F分别是▱ABCD的边BC、AD上的点,且BE=DF.
(1)、表中a、b、c、d分别为:a=; b=; c=; d=.(2)、补全频数分布直方图;(3)、如果某天该路段约有1500辆通过,汽车时速不低于60千米即为违章,通过该统计数据估计当天违章车辆约有多少辆?23. 如图,E、F分别是▱ABCD的边BC、AD上的点,且BE=DF.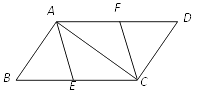 (1)、求证:四边形AECF是平行四边形;
(1)、求证:四边形AECF是平行四边形;
(2)、若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.24. 某市从今年1月1日起调整水价,每立方米水费上涨了原价的 .据了解,某校去年11月份的水费是1800元,而今年1月份的水费是3600元.如果该校今年1月份的用水量比去年11月份的用水量多600m3 .
(1)、该市原来每立方米水价是多少元?(2)、该校开展了“节约每一滴水”的主题活动,采取了有效的节约用水措施,计划今年5月份的用水量较1月份降低20%,那么该校今年5月份应交的水费是多少?25. 如图,一次函数y=﹣x+5的图象与反比例函数y= (k≠0)在第一象限的图象交于A(1,n)和B两点. (1)、求反比例函数的解析式与点B坐标;(2)、求△AOB的面积;(3)、在第一象限内,当一次函数y=﹣x+5的值小于反比例函数y= (k≠0)的值时,写出自变量x的取值范围.26. 如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.
(1)、求反比例函数的解析式与点B坐标;(2)、求△AOB的面积;(3)、在第一象限内,当一次函数y=﹣x+5的值小于反比例函数y= (k≠0)的值时,写出自变量x的取值范围.26. 如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.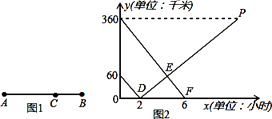 (1)、填空:A,B两地相距千米;(2)、求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;(3)、当客车行驶多长时间,客、货两车相距150千米.27. 在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.
(1)、填空:A,B两地相距千米;(2)、求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;(3)、当客车行驶多长时间,客、货两车相距150千米.27. 在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.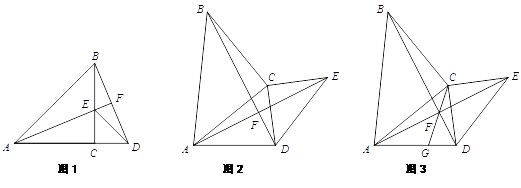 (1)、如图1,当点A、C、D在同一条直线上时,AC=12,EC=5.
(1)、如图1,当点A、C、D在同一条直线上时,AC=12,EC=5.①求证:AF⊥BD,
②求AF的长度;
(2)、如图2,当点A、C、D不在同一条直线上时.求证:AF⊥BD;(3)、如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数,若不是,请说明理由.28. 如图,直线y=-x+4与x轴、y轴分别交于A、B两点,直线BC与x轴、y轴分别交于C、B两点,连接BC,且 .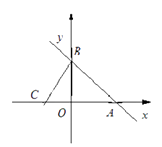
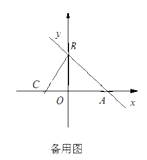
 (1)、求点A的坐标及直线BC的函数关系式;(2)、点M在x轴上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;(3)、若点P在x轴上,平面内是否存在点Q,使点B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
(1)、求点A的坐标及直线BC的函数关系式;(2)、点M在x轴上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;(3)、若点P在x轴上,平面内是否存在点Q,使点B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.