2017-2018学年浙教版八年级上学期期末复习试卷
试卷更新日期:2018-01-23 类型:期末考试
一、单选题
-
1. 若三角形两条边的长度分别是3cm和7cm,则第三条边的长度可能是( )A、3cm B、4cm C、5cm D、10cm2. 不等式2x﹣2<0的解集是( )A、x<1 B、x<﹣1 C、x>1 D、x>﹣13. 点A(﹣1,2)与A′关于x轴对称,则点A′的坐标是( )A、(1,2) B、(1,﹣2) C、(﹣1,﹣2) D、(﹣1,2)4. 可以用来说明命题“若m<n,则 ”是假命题的反例是( )A、m=2,n=﹣3 B、m=﹣2,n=3 C、m=﹣2,n=﹣3 D、m=2,n=35. 等腰三角形的一个外角等于130°,则这个等腰三角形的底角为( )A、65° B、50° C、65°或40° D、50°或65°6. 一次函数y=x﹣2的图象大致是( )A、
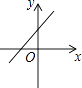 B、
B、 C、
C、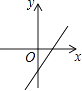 D、
D、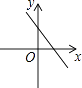 7. 在Rt△ABC中,∠C=90°,当△ABC沿折痕BE翻折时,点C恰好落在AB的中点D上,若BE=4,则AC的长是( )
7. 在Rt△ABC中,∠C=90°,当△ABC沿折痕BE翻折时,点C恰好落在AB的中点D上,若BE=4,则AC的长是( )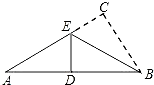 A、4 B、6 C、8 D、108.
A、4 B、6 C、8 D、108.如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,则点D的坐标是( )
 A、(4,8) B、(5,8) C、( , ) D、( , )9.
A、(4,8) B、(5,8) C、( , ) D、( , )9.在△ABC中,∠BAC=90°,AB=3,AC=4.AD平分∠BAC交BC于D,则BD的长为
 A、 B、 C、 D、10.
A、 B、 C、 D、10.如图,点A,B,C在一次函数y=﹣2x+m的图象上,它们的横坐标依次为﹣1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
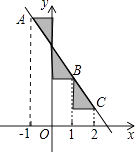 A、3(m﹣1) B、 C、1 D、311.
A、3(m﹣1) B、 C、1 D、311.已知△ABC是斜边长为1cm的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,第n个等腰直角三角形的斜边长是( )
 A、cm B、cm C、cm D、cm12.
A、cm B、cm C、cm D、cm12.如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是( )
 A、8 B、10 C、 D、
A、8 B、10 C、 D、二、填空题
-
13. 函数y= 中,自变量x的取值范围是 .14. 用不等式表示“m的4倍与7的和是负数”是 .15. 将如图所示的一块直角三角板放置在△ABC上,使三角板的两条直角边DE、EF分别经过点B、C,若∠A=65°,则∠ABE+∠ACE= .
 16. 如图所示的一块地,∠ADC=90°,AD=3m,CD=4m,AB=13m,BC=12m,则这块地的面积是 m2 .
16. 如图所示的一块地,∠ADC=90°,AD=3m,CD=4m,AB=13m,BC=12m,则这块地的面积是 m2 .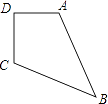 17. 如图,函数y=2x和y=ax+4的图象相交于A(m,3),则不等式2x<ax+4的解为 .
17. 如图,函数y=2x和y=ax+4的图象相交于A(m,3),则不等式2x<ax+4的解为 .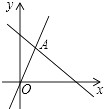 18. 在一次“人与环境”知识竞赛中,共有25个题,每题四个答案,其中只有一个答案正确,每选对一题得4分,不选或选错倒扣2分,如果一个学生在本次竞赛中得分不低于60分,那么他至少要答对题.19. 如图,点E在边长为4的正方形ABCD的边AD上,点A关于BE的对称点为A′,延长EA′交DC于点F,若CF=1cm,则AE=m.
18. 在一次“人与环境”知识竞赛中,共有25个题,每题四个答案,其中只有一个答案正确,每选对一题得4分,不选或选错倒扣2分,如果一个学生在本次竞赛中得分不低于60分,那么他至少要答对题.19. 如图,点E在边长为4的正方形ABCD的边AD上,点A关于BE的对称点为A′,延长EA′交DC于点F,若CF=1cm,则AE=m.
三、解答题
-
20. 利用数轴,解一元一次不等式组: .
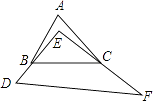
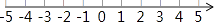 21. 如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.求证:MN=CN﹣BM.
21. 如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.求证:MN=CN﹣BM. 22. 如图,已知四边形ABCD中,AC平分∠BAD,AB=AC=5,AD=3,BC=CD.求点C到AB的距离.
22. 如图,已知四边形ABCD中,AC平分∠BAD,AB=AC=5,AD=3,BC=CD.求点C到AB的距离.
四、综合题
-
23. 如图所示,△ABC的顶点分别为A(-4, 5),B(﹣3, 2),C(4,-1).
 (1)、作出△ABC关于x轴对称的图形△A1B1C1;(2)、写出A1、B1、C1的坐标;(3)、若AC=10,求△ABC的AC边上的高.24. 某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
(1)、作出△ABC关于x轴对称的图形△A1B1C1;(2)、写出A1、B1、C1的坐标;(3)、若AC=10,求△ABC的AC边上的高.24. 某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:原料
维生素C及价格
甲种原料
乙种原料
维生素C(单位/千克)
600
400
原料价格(元/千克)
9
5
现要配制这种营养食品20千克,要求每千克至少含有9600单位的维生素C.设购买甲种原料x千克.
(1)、至少需要购买甲种原料多少千克?(2)、设食堂用于购买这两种原料的总费用为y元,求y与x的函数关系式.并说明购买甲种原料多少千克时,总费用最少?最少费用是多少?25. 在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0),点P是直线AB上的一个动点,记点P关于y轴对称的点为P′.(1)、当b=3时(如图1),

①求直线AB的函数表达式.
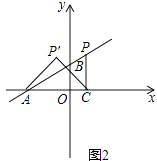
(2)、②在x轴上找一点Q(点O除外),使△APQ与△AOB全等,直接写出点Q的所有坐标(3)、若点P在第一象限(如图2),设点P的横坐标为a,作PC⊥x轴于点C,连结AP′,CP′.当△ACP′是以点P′为直角顶点的等腰直角三角形时,求出a,b的值.
 (4)、
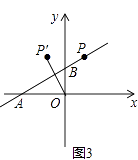
(4)、当线段OP′恰好被直线AB垂直平分时(如图3),直接写出b= .
五、作图题
-
26.
已知:如图△ABC .
求作:①AC边上的高BD;
②△ABC的角平分线CE .
