山东省东营市河口区2017届九年级上册数学期末考试试卷

试卷更新日期：2018-01-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中既是中心对称图形又是轴对称图形的是（）

A、 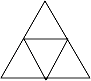B、 C、 D、

查看试题解析
2. 点（2，﹣4）在反比例函数y= $\frac{k}{x}$ 的图象上，则下列各点在此函数图象上的是（）

A、（2，4） B、（﹣1，﹣8） C、（﹣2，﹣4） D、（4，﹣2）

查看试题解析
3. 某校九年级共有1、2、3、4四个班，现从这四个班中随机抽取两个班进行一场篮球比赛，则恰好抽到1班和2班的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{3}{8}$ D、 $\frac{1}{2}$

查看试题解析
4. 如图，AD∥BE∥CF，直线l₁、l₂这与三条平行线分别交于点A，B，C和点D，E，F．已知AB=1，BC=3，DE=2，则EF的长为（）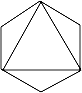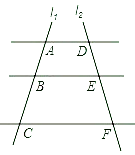

A、4 B、5 C、6 D、8

查看试题解析
5. 如图，小雅家（图中点O处）门前有一条东西走向的公路，经测得有一水塔（图中点A处）在距她家北偏东60°方向的500米处，那么水塔所在的位置到公路的距离AB是（）

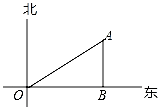A、250米 B、250 $\sqrt{3}$ 米 C、 $\frac{500}{3} \sqrt{3}$ 米 D、500 $\sqrt{2}$ 米

查看试题解析
6. 如图，圆锥的底面半径r为6cm，高h为8cm，则圆锥的侧面积为（）

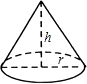A、30πcm² B、48πcm² C、60πcm² D、80πcm²

查看试题解析
7. 如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是（）

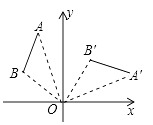A、（5，2） B、（2，5） C、（2，﹣5） D、（5，﹣2）

查看试题解析
8.
如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：
①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠CAD= $\sqrt{2}$ ．
其中正确的结论有（）

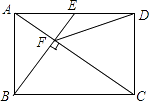A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

9. 已知反比例函数y= $\frac{k}{x}$ （k为常数，k≠0）的图象位于第一、第三象限，写出一个符合条件的k的值为．

查看试题解析
10. 抛物线y=x²+2x+m﹣1与x轴有两个不同的交点，则m的取值范围是．

查看试题解析
11. 在﹣2，﹣1，0，1，2这五个数中任取两数m，n，则二次函数y=（x﹣m）²+n的顶点在坐标轴上的概率为

查看试题解析
12. 如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD=90°，CO=CD．若B（1，0），则点C的坐标为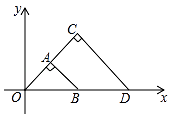

查看试题解析
13. 如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为30°，测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平距离AD为90米，那么该建筑物的高度BC约为米(精确到1米，参考数据： $\sqrt{3}$ ≈1.73)．

查看试题解析
14. 如图，以AB为直径，点O为圆心的半圆经过点C，若AC=BC= $\sqrt{2}$ ，则图中阴影部分的面积是．

查看试题解析
15. 如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为

查看试题解析
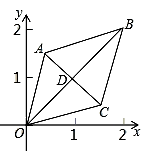16. 如图，分别用火柴棍连续搭建正三角形和正六边形，公共边只用一根火柴棍．如果搭建正三角形和正六边形共用了2016根火柴棍，并且正三角形的个数比正六边形的个数多6个，那么能连续搭建正三角形的个数是

查看试题解析

三、解答题

17. 计算题

(1)、计算： ${(- \frac{1}{2})}^{- 2} - | \sqrt{3} - 2 | + {(\sqrt{2} - 1.414)}^{0} - 3 tan 30 ° - \sqrt{{(- 2)}^{2}}$ ．

(2)、先化简，再求值： $\frac{m - 3}{3 m^{2} - 9 m} \div \frac{1}{3 m^{2}}$ ，其中m是二次函数 $y = {(x + 2)}^{2} - 3$ 顶点的纵坐标．

查看试题解析
18. 一个不透明的袋中装有20个只有颜色不同的球，其中5个黄球，8个黑球，7个红球．

(1)、求从袋中摸出一个球是黄球的概率；

(2)、现从袋中取出若干个黑球，搅匀后，使从袋中摸出一个球是黑球的概率是 $\frac{1}{3}$ ，求从袋中取出黑球的个数．

查看试题解析
19. 南沙群岛是我国的固有领土，现在我南海渔民要在南沙群岛某海岛附近进行捕鱼作业，当渔船航行至B处时，测得该岛位于正北方向20（1＋ $\sqrt{3}$ ）海里的C处，为防止某国的巡警干扰，就请求我A处的鱼监船前往C处护航，已知C位于A处的北偏东45°方向上，A位于B的北偏西30°的方向上，求A、C之间的距离．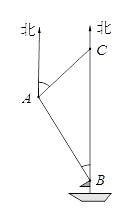

查看试题解析
20. 某地区2014年投入教育经费2 500万元，2016年投入教育经费3025万元．

(1)、求2014年至2016年该地区投入教育经费的年平均增长率；

(2)、根据(1)所得的年平均增长率，预计2017年该地区将投入教育经费多少万元？

查看试题解析
21. 如图，点O在∠APB的平分线上，⊙O与PA相切于点C．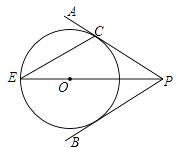

(1)、求证：直线PB与⊙O相切；

(2)、PO的延长线与⊙O交于点E．若⊙O的半径为3，PC=4．求弦CE的长．

查看试题解析
22. 如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，与反比例函数 $y = \frac{m}{x}$ 的图象在第二象限交于点C，CE垂直于x轴，垂足为点E， $tan ∠ A B O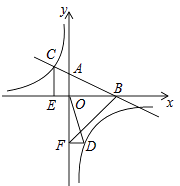 = \frac{1}{2}$ ，OB=4，OE=2.

(1)、求反比例函数的解析式；

(2)、若点D是反比例函数图象在第四象限上的点，过点D做DF垂直于y轴，垂足为点F，连接OD、BF，如果 $S_{Δ B A F} = 4 S_{Δ D F O}$ ，求点D的坐标．

查看试题解析
23. 如图，已知点O (0，0)，A (－5，0)，B (2，1)，抛物线 $l ： y = - {(x - h)}^{2} + 1$ (h为常数)与y轴的交点为C。

(1)、抛物线经过点B，求它的解析式，并写出此时抛物线的对称轴及顶点坐标；

(2)、设点C的纵坐标为 $y_{C}$ ，求 $y_{C}$ 的最大值，此时抛物线上有两点 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ，其中 $x_{1} > x_{2} \geq 0$ ，比较 $y_{1}$ 与 $y_{2}$ 的大小；

(3)、当线段OA被只分为两部分，且这两部分的比是1：4时，求h的值。

查看试题解析