内蒙古满洲里市2017届九年级上册数学期末考试试卷
试卷更新日期:2018-01-23 类型:期末考试
一、单选题
-
1. 下列汉字或字母中既是中心对称图形又是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 2. 一元二次方程 根的情况是( )
2. 一元二次方程 根的情况是( )
A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定3. 方程x2=3x的解是( )
A、x=3 B、x=0 C、x1=-3, x2=0 D、x1=3, x2=04. 抛物线 的顶点坐标是( )
A、(2,-3) B、(-2,3) C、(2,3) D、(-2,-3)5. 在双曲线y= 的任一支上,y都随x的增大而增大,则k的值可以是( )A、2 B、0 C、﹣2 D、16. 下列成语中,属于随机事件的是( )
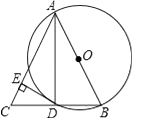
A、水中捞月 B、瓮中捉鳖 C、守株待兔 D、探囊取物7. 如图,已知⊙O中∠AOB度数为100°,C是圆周上的一点,则∠ACB的度数为( )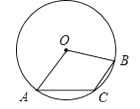 A、130° B、100° C、80° D、50°8. 下列四个命题中,正确的个数是( )
A、130° B、100° C、80° D、50°8. 下列四个命题中,正确的个数是( )①经过三点一定可以画圆;
②任意一个三角形一定有一个外接圆;
③三角形的内心是三角形三条角平分线的交点;
④三角形的外心到三角形三个顶点的距离都相等;
⑤三角形的外心一定在三角形的外部.
A、4个 B、3个 C、2个 D、1个9. 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为( )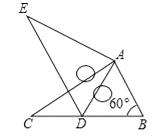 A、0.5 B、1.5 C、
A、0.5 B、1.5 C、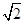 D、1
10. 某地区为估计该地区黄羊的只数,先捕捉20只黄羊给它们分别作上标志,然后放回,待有标志的黄羊完全混合于黄羊群后,第二次捕捉40只黄羊,发现其中两只有标志.从而估计该地区有黄羊( )A、200只 B、400只 C、800只 D、1000只11. 某种药品原价为49元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
D、1
10. 某地区为估计该地区黄羊的只数,先捕捉20只黄羊给它们分别作上标志,然后放回,待有标志的黄羊完全混合于黄羊群后,第二次捕捉40只黄羊,发现其中两只有标志.从而估计该地区有黄羊( )A、200只 B、400只 C、800只 D、1000只11. 某种药品原价为49元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
A、49(1﹣x)2=49﹣25 B、49(1﹣2x)=25 C、49(1﹣x)2=25 D、49(1﹣x2)=2512. 二次函数y=ax2+bx+c的图象如图所示,则反比例函数 与一次函数y=bx+c在同一坐标系中的大致图象是( )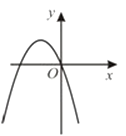 A、
A、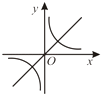 B、
B、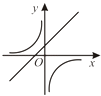 C、
C、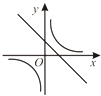 D、
D、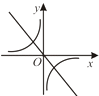
二、填空题
-
13. 有一个边长为3的正六边形,若要剪一张圆形纸片完全盖住这个圆形,则这个圆形纸片的半径最小是 .
14. 已知一个布袋里装有2个红球,3个白球和1个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为 .
15. 如图,过反比例函数 (x>0)的图象上一点A作AB⊥x轴于点B,连接AO,若S△AOB=2,则k的值为 .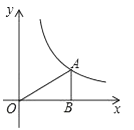 16. 已知函数
16. 已知函数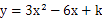 (k为常数)的图象经过点A(1,
(k为常数)的图象经过点A(1,  ), B(2,
), B(2, 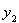 ),C(-3,
),C(-3, 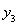 ),则
),则  ,
, 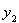 ,
, 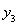 从小到大排列顺序为
从小到大排列顺序为
17. 如图,一男生推铅球,铅球行进高度 (米)与水平距离 (米)之间的关系是 ,则铅球推出距离米.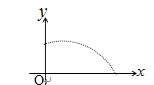 18. 有一半径为1m的圆形铁片,要从中剪出一个最大的圆心角为90°的扇形ABC,用来围成一个圆锥,该圆锥底面圆的半径是 .
18. 有一半径为1m的圆形铁片,要从中剪出一个最大的圆心角为90°的扇形ABC,用来围成一个圆锥,该圆锥底面圆的半径是 .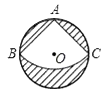
三、解答题
-
19. 解方程:
(1)、(2)、
20. 如图,在平面直角坐标系中,O为原点,一次函数y1=x+m与反比例函数y2= 的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C. (1)、求反比例函数解析式和点B坐标;(2)、当x的取值范围是时,有y1>y2 .21. 如图,在以点O为圆心的两个圆中,大圆的弦AB交小圆于点C、D,求证:AC=BD.
(1)、求反比例函数解析式和点B坐标;(2)、当x的取值范围是时,有y1>y2 .21. 如图,在以点O为圆心的两个圆中,大圆的弦AB交小圆于点C、D,求证:AC=BD.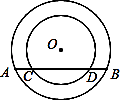 22. 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1 .
22. 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1 .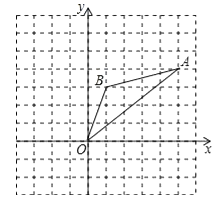 (1)、画出△A1OB1;(2)、在旋转过程中点B所经过的路径长为;
(1)、画出△A1OB1;(2)、在旋转过程中点B所经过的路径长为;
(3)、求在旋转过程中线段AB、BO扫过的图形的面积之和.
23. 甲乙两同学用一副扑克牌中牌面数字分别是3,4,5,6的4张牌做抽数字游戏,游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,抽出的牌不放回,然后将剩下的牌洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数,若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请利用树状图或列表法说明理由.
24. 某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.
(1)、若商场平均每天盈利1200元,每件衬衣应降价多少元?(2)、若要使商场平均每天的盈利最多,请你为商场设计降价方案.