江苏省苏州市相城区2017届九年级上册数学期末考试试卷
试卷更新日期:2018-01-23 类型:期末考试
一、单选题
-
1. 在一副扑克牌(54张,其中王牌两张)中,任意抽取一张牌是“王牌”的概率是( )A、 B、 C、 D、2. 抛物线 的对称轴是( )A、直线 B、直线 C、直线 D、3. 下列方程有实数根的是( )A、 B、 C、 D、4. 如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,AQ=20cm,则CQ的长是( )
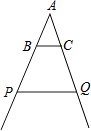 A、8cm B、12cm C、30cm D、50cm5. 对于一组数据﹣1、4、﹣1、2下列结论不正确的是( )A、平均数是1 B、众数是-1 C、中位数是0.5 D、方差是3.56. 如图,第一象限的点P的坐标是(3,4),则tan 等于( )
A、8cm B、12cm C、30cm D、50cm5. 对于一组数据﹣1、4、﹣1、2下列结论不正确的是( )A、平均数是1 B、众数是-1 C、中位数是0.5 D、方差是3.56. 如图,第一象限的点P的坐标是(3,4),则tan 等于( ) A、 B、 C、 D、7. 如图,若AB是⊙O的直径,CD是⊙O的弦, ,则 的度数是( )
A、 B、 C、 D、7. 如图,若AB是⊙O的直径,CD是⊙O的弦, ,则 的度数是( ) A、35° B、45° C、55° D、75°8. 如图,直线 与 轴、 轴分别交于点A、B,点C在X轴上, ,则点C的坐标是( )
A、35° B、45° C、55° D、75°8. 如图,直线 与 轴、 轴分别交于点A、B,点C在X轴上, ,则点C的坐标是( ) A、 B、 C、 D、9. 如图,在 中, ,tan ,AB=6cm.动点P从点A开始沿边AB向点B以1 cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中, 的最大面积是( )
A、 B、 C、 D、9. 如图,在 中, ,tan ,AB=6cm.动点P从点A开始沿边AB向点B以1 cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中, 的最大面积是( )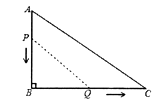 A、18cm2 B、12cm2 C、9cm2 D、3cm210. 已知二次函数 的图像经过点 ,则 有( )A、最小值 B、最小值 C、最大值 D、最大值
A、18cm2 B、12cm2 C、9cm2 D、3cm210. 已知二次函数 的图像经过点 ,则 有( )A、最小值 B、最小值 C、最大值 D、最大值二、填空题
-
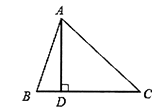
11. 已知圆锥的底面半径为3,高为4,则这个圆锥的母线长为.12. 如图,在 中, ,垂足为点 ,若 ,则 =.
 13. 若两个等边三角形的边长分别为 与3 ,则它们的面积之比为.
13. 若两个等边三角形的边长分别为 与3 ,则它们的面积之比为.
14. 已知a、b是一元二次方程 的两个实数根,则 的值是.15. 某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、"10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率.
16. 若二次函数 的图像的对称轴是直线 ,则关于 的方程 的解为.17. 如图,为了测得电视塔的高度 ,在 处用高为1米的测角仪 ,测得电视塔顶端 的仰角为30°,再向电视塔方向前进100米到达 处,又测得电视塔顶端 的仰角为60°,则这个电视塔的高度 为米(结果保留根号). 18. 抛物线 的顶点为 ,与 轴的一个交点 在点(-3, 0)和(-2 ,0)之间,其部分图象如图,则以下结论:① <0 ;② <0;③ =2;④方程 有两个相等的实数根,其中正确结论的个数为个.
18. 抛物线 的顶点为 ,与 轴的一个交点 在点(-3, 0)和(-2 ,0)之间,其部分图象如图,则以下结论:① <0 ;② <0;③ =2;④方程 有两个相等的实数根,其中正确结论的个数为个.
三、解答题
-
19. 计算: .20. 解方程: .21. 如图, ∽ .
 (1)、求 的大小;(2)、求 的长.22. 如图, 是⊙ 的直径, 是⊙ 的弦,过点 的切线交 的延长线于点 ,且 .
(1)、求 的大小;(2)、求 的长.22. 如图, 是⊙ 的直径, 是⊙ 的弦,过点 的切线交 的延长线于点 ,且 . (1)、求 的度数;(2)、若 =3,求图中阴影部分的面积.23. 某校为了解学生“自主学习、合作交流” 的情况,对某班部分同学进行了一段时间的跟踪调查,将调查结果(A:特别好;B:好;C:一般;D:较差)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)、求 的度数;(2)、若 =3,求图中阴影部分的面积.23. 某校为了解学生“自主学习、合作交流” 的情况,对某班部分同学进行了一段时间的跟踪调查,将调查结果(A:特别好;B:好;C:一般;D:较差)绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题: (1)、补全条形统计图;
(1)、补全条形统计图;
(2)、扇形统计图中,求 类所占圆心角的度数;(3)、学校想从被调查的 类(1名男生2名女生)和D类(男女生各占一半)中分别选取一位同学进行“一帮一”互助学习,请用画树形图或列表的方法求所选的两位同学恰好是一男一女的概率.24. 为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面 与通道 平行),通道水平宽度 为8米, ,通道斜面 的长为6米,通道斜面 的坡度 . (1)、求通道斜面 的长为米;(2)、为增加市民行走的舒适度,拟将设计图中的通道斜面 的坡度变缓,修改后的通道斜面 的坡角为30°,求此时 的长.(结果保留根号)25. 某农场去年种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为 .
(1)、求通道斜面 的长为米;(2)、为增加市民行走的舒适度,拟将设计图中的通道斜面 的坡度变缓,修改后的通道斜面 的坡角为30°,求此时 的长.(结果保留根号)25. 某农场去年种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为 .
(1)、则今年南瓜的种植面积为亩;(用含 的代数式表示)
(2)、如果今年南瓜亩产量的增长率是种植面积的增长率的 ,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
26. 二次函数 的图象与 轴交于 (1, 0), 两点,与 轴交于点 ,其顶点 的坐标为(-3, 2). (1)、求这二次函数的关系式;(2)、求 的面积.
(1)、求这二次函数的关系式;(2)、求 的面积.
27. 如图, 是⊙ 的直径, 、 为⊙ 上位于 异侧的两点,连接 并延长至点 ,使得 ,连接 交⊙ 于点 ,连接 、 、 . (1)、证明: ;(2)、若 ,求 的度数;(3)、设 交 于点 ,若 是 的中点,求 的值.28. 如图,二次函数y=ax2-6ax+4a+3的图像与y轴交于点A,点B是x轴上一点,其坐标为(1,0),连接AB,tan∠ABO=2.
(1)、证明: ;(2)、若 ,求 的度数;(3)、设 交 于点 ,若 是 的中点,求 的值.28. 如图,二次函数y=ax2-6ax+4a+3的图像与y轴交于点A,点B是x轴上一点,其坐标为(1,0),连接AB,tan∠ABO=2. (1)、则点A的坐标为 , a=;(2)、过点A作AB的垂线与该二次函数的图象交于另一点C,求点C的坐标;(3)、连接BC,过点A作直线l交线段BC于点P,设点B、点C到l的距离分别为d1、d2 , 求d1+d2的最大值.
(1)、则点A的坐标为 , a=;(2)、过点A作AB的垂线与该二次函数的图象交于另一点C,求点C的坐标;(3)、连接BC,过点A作直线l交线段BC于点P,设点B、点C到l的距离分别为d1、d2 , 求d1+d2的最大值.