江西省上饶市婺源县2017届九年级上册数学期末考试试卷
试卷更新日期：2018-01-23 类型：期末考试
一、单选题
-
1. 一元二次方程x2－x－2＝0的解是（ ）
A、x1＝1，x2＝2 B、x1＝1，x2＝－2 C、x1＝－1，x2＝－2 D、x1＝－1，x2＝22. 对于二次函数y=（x﹣1）2+2的图象，下列说法正确的是（ ）A、开口向下 B、对称轴是x=﹣1 C、顶点坐标是（1，2） D、与x轴有两个交点3. 下列图形是中心对称图形而不是轴对称图形的是（ ）A、
B、
C、
D、
4. 如图，线段AB是⊙O的直径，弦CD丄AB，∠CAB=20°，则∠BOD等于（ ）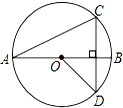
A、20° B、30° C、40° D、60°5. 下列事件是必然事件的是（ ）A、抛掷一枚硬币四次，有两次正面朝上 B、打开电视频道，正在播放《十二在线》 C、射击运动员射击一次，命中十环 D、方程x2﹣2x﹣1=0必有实数根6. 关于x的方程（a －5）x2－4x－1＝0有实数根，则a满足（ ）
A、a≥1 B、a＞1且a≠5 C、a≥1且a≠5 D、a≠57. 已知二次函数y=ax2+bx+c的图象如图，则下列叙述正确的是（ ）
A、abc＜0 B、﹣3a+c＜0 C、b2﹣4ac≥0 D、将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c8. 在同一坐标系中，一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是（ ）
A、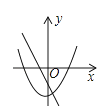
B、
C、
D、
9. 某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（ ）
A、560(1＋x)2＝315 B、560(1－x)2＝315 C、560(1－2x)2＝315 D、560(1－x2)＝31510. 如图，已知AB是⊙O的直径，AD切⊙O于点A，点C是 的中点，则下列结论：①OC∥AE；②EC＝BC；③∠DAE＝∠ABE；④AC⊥OE，其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 将抛物线y=x2向左平移5个单位，得到的抛物线解析式为 ．12. 已知m，n是方程x2+2x﹣5=0的两个实数根，则m﹣mn+n= ．13. 用半径为3cm，圆心角是120°的扇形围成一个圆锥的侧面，这个圆锥底面半径为。
14. 如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是。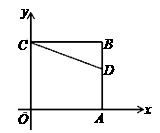
15. 在一个不透明的盒子中装有16个白球，若干个黄球，它们除了颜色不同外，其余均相同，若从中随机摸出一个球是黄球的概率是 ，则黄球的个数为 ．16. 如图是二次函数y＝ax2＋bx＋c图象的一部分，图象过点A（－3，0），对称轴为直线x＝－1，给出四个结论：①b2＞4ac；②2a＋b＝0；③a＋b＋c＞0；④若点B（ ，y1），C（ ，y2）为函数图象上的两点，则y1＜y2 ． 其中正确结论是 ．
三、解答题
-
17. 解方程：x2－5 = 4x．18. 如图，△ABC的顶点都在方格线的交点（格点）上．
(1)、①将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′，请在图中画出△A′B′C′．②将△ABC向上平移1个单位，再向右平移5个单位得到△A″B″C″，请在图中画出△A″B″C″．
(2)、若将△ABC绕原点O旋转180°，A的对应点A1的坐标是 ．
19. 四张扑克牌（方块2、黑桃4、黑桃5、梅花5）的牌面如图l，将扑克牌洗匀后，如图2背面朝上放置在桌面上．小亮和小明设计的游戏规则是两人同时抽取一张扑克牌，两张牌面数字之和为奇数时，小亮获胜；否则小明获胜．请问这个游戏规则公平吗？并说明理由．
20. 某小区在绿化工程中有一块长为20m、宽为8m的矩形空地，计划在其中修建两块相同的矩形绿地，使它们的面积之和为56m2 ， 两块绿地之间及周边留有宽度相等的人行通道（如图所示），求人行通道的宽度．
21. 用工件槽（如图1）可以检测一种铁球的大小是否符合要求，已知工件槽的两个底角均为90°，尺寸如图（单位：cm）．将形状规则的铁球放入槽内时，若同时具有图1所示的A、B、E三个接触点，该球的大小就符合要求．图2是过球心O及A、B、E三点的截面示意图，求这种铁球的直径．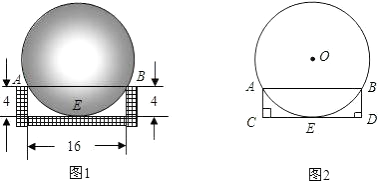
22. 已知AB是⊙O的直径，⊙O过BC的中点D，且DE垂直AC于E．
(1)、求证：AB=AC；(2)、求证：DE是⊙O的切线；(3)、若AB=13，BC=10，求DE的长23. 如图，抛物线y=x2+bx+c与x轴交于A（-1，0），B（3，0）两点．
(1)、求该抛物线的解析式；(2)、求该抛物线的对称轴以及顶点坐标；(3)、设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S△PAB=8，并求出此时P点的坐标．24. 某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
(1)、求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；
(2)、求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？(3)、如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本＝每件的成本×每天的销售量）
25. 如图，抛物线y＝－x2－2x＋3的图象与x轴交于A、B两点(点A在点B的左边)，与y轴交于点C，点D为抛物线的顶点．
(1)、求点A、B、C的坐标；(2)、点M为线段AB上一点(点M不与点A、B重合)，过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；
(3)、在(2)的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作y轴的平行线，与直线AC交于点G(点G在点F的上方)．若， 求点F的坐标．