辽宁省铁岭市2017届九年级上册数学期末考试试卷
试卷更新日期:2018-01-23 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,二次函数y=a(x−h)2(a≠0)的图象可能是( )A、
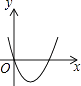 B、
B、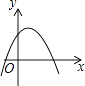 C、
C、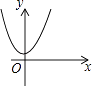 D、
D、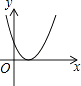 2. 已知两点(x1 , y1),(x2 , y2) 在函数y= - 的图象上,当x1>x2>0时,下列结论正确的是( )A、y1>y2>0 B、y1<y2<0 C、y2>y1>0 D、y2<y1<03. 一元二次方程x2-2x+1=0的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根4. 如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则弧BC的长是( )
2. 已知两点(x1 , y1),(x2 , y2) 在函数y= - 的图象上,当x1>x2>0时,下列结论正确的是( )A、y1>y2>0 B、y1<y2<0 C、y2>y1>0 D、y2<y1<03. 一元二次方程x2-2x+1=0的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根4. 如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则弧BC的长是( )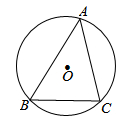 A、 π B、 π C、 π D、 π5. 如图,在平行四边形ABCD中,E为CD上一点,连接AE,BD,且AE,BD相交于点F,DE:EC=2:3,则S△DEF:S△ABF等于( )
A、 π B、 π C、 π D、 π5. 如图,在平行四边形ABCD中,E为CD上一点,连接AE,BD,且AE,BD相交于点F,DE:EC=2:3,则S△DEF:S△ABF等于( ) A、4:25 B、4:9 C、9:25 D、2:36. 在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任可其他区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的频率是0.2,则估计盒子中大约有红球( )
A、4:25 B、4:9 C、9:25 D、2:36. 在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任可其他区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的频率是0.2,则估计盒子中大约有红球( )
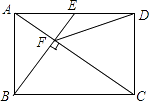
A、16个 B、20个 C、25个 D、30个7.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= .
其中正确的结论有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
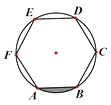
8. 如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为2 ,则图中阴影部分的面积为.
 9. 如图,在A处看建筑物CD的顶端D的仰角为α,则tanα=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为米.
9. 如图,在A处看建筑物CD的顶端D的仰角为α,则tanα=0.7,向前行进3米到达B处,从B处看D的仰角为45°(图中各点均在同一平面内,A、B、C三点在同一条直线上,CD⊥AC),则建筑物CD的高度为米.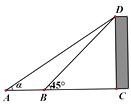 10. 2路公交车每隔5分钟发一班车,豆豆来到2路公交站牌,候车时间不少于2分钟的概率为.11. 关于x的一元二次方程x2+bx+c=0的两根为x1=1,x2=2,那么抛物线y=x2+bx+c的顶点坐标为.
10. 2路公交车每隔5分钟发一班车,豆豆来到2路公交站牌,候车时间不少于2分钟的概率为.11. 关于x的一元二次方程x2+bx+c=0的两根为x1=1,x2=2,那么抛物线y=x2+bx+c的顶点坐标为.
12. 某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为元时,该服装店平均每天的销售利润最大.13. 如图,已知△ABC中,AB=5,AC=3,点D在边AB上,且∠ACD=∠B,则线段AD的长为 .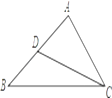 14. 如图,分别过反比例函数y= 的图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn)…作x轴的垂线,垂足分别为A1 , A2 , …,An…,连接A1P2 , A2P3 , …,An-1Pn , …,再以A1P1 , A1P2为一组邻边画一个平行四边形A1P1B1P2 , 以A 2P2 , A2P3为一组邻边画一个平行四边形A2P2B2P3 , 点B2的纵坐标是.依此类推,则点Bn的纵坐标是.(结果用含n代数式表示)
14. 如图,分别过反比例函数y= 的图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn)…作x轴的垂线,垂足分别为A1 , A2 , …,An…,连接A1P2 , A2P3 , …,An-1Pn , …,再以A1P1 , A1P2为一组邻边画一个平行四边形A1P1B1P2 , 以A 2P2 , A2P3为一组邻边画一个平行四边形A2P2B2P3 , 点B2的纵坐标是.依此类推,则点Bn的纵坐标是.(结果用含n代数式表示)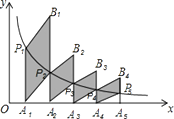
三、解答题
-
15. 如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2 , 两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米.
 16. 已知α是锐角,且cos(α-15°)= ,计算 -6cosα+(3-π)0+tanα-( )-1的值.17. 如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,
16. 已知α是锐角,且cos(α-15°)= ,计算 -6cosα+(3-π)0+tanα-( )-1的值.17. 如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,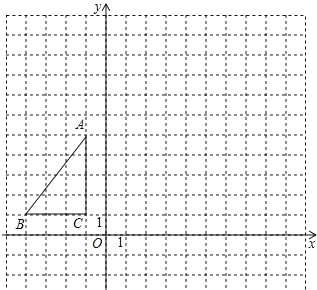 (1)、画出△AB′C′;
(1)、画出△AB′C′;
(2)、写出点B′,C′的坐标;
(3)、求出在△ABC旋转的过程中,点C经过的路径长.
18. 为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题: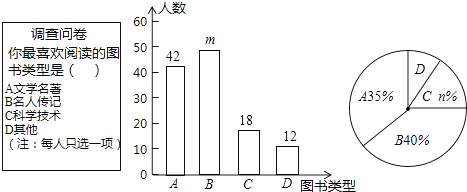 (1)、本次调查共抽查了名学生,两幅统计图中的m= , n=.(2)、已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?(3)、学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?19. 如图,已知一次函数y= x-3与反比例函数y= 的图象相交于点A(4,n),与x轴相交于点B.
(1)、本次调查共抽查了名学生,两幅统计图中的m= , n=.(2)、已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?(3)、学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?19. 如图,已知一次函数y= x-3与反比例函数y= 的图象相交于点A(4,n),与x轴相交于点B. (1)、填空:n的值为 , k的值为;(2)、以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;(3)、观察反比函数y= 的图象,当y≥-2时,请直接写出自变量x的取值范围.
(1)、填空:n的值为 , k的值为;(2)、以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;(3)、观察反比函数y= 的图象,当y≥-2时,请直接写出自变量x的取值范围.
20. 如图,三沙市一艘海监船某天在黄岩鸟P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据: ≈1.414,结果精确到0.1)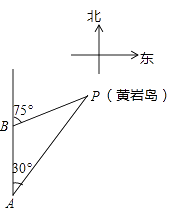 21. 如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
21. 如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.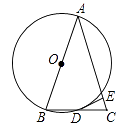 (1)、求证:DE为⊙O的切线;(2)、若AB=13,sinB= ,求DE的长.
(1)、求证:DE为⊙O的切线;(2)、若AB=13,sinB= ,求DE的长.
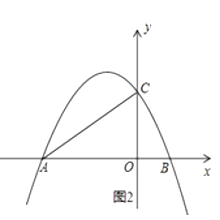
22. 如图,在平面直角坐标系中,抛物线y=ax2+bx+ 与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,点D与点C关于抛物线的对称轴对称.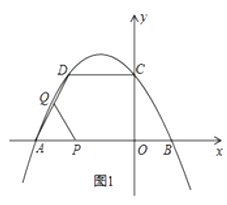 (1)、求抛物线的解析式,并直接写出点D的坐标;(2)、如图1,点P从点A出发,以每秒1个单位长度的速度沿A→B匀速运动,到达点B时停止运动.以AP为边作等边△APQ(点Q在x轴上方).设点P在运动过程中,△APQ与四边形AOCD重叠部分的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式;(3)、如图2,连接AC,在第二象限内存在点M,使得以M、O、A为顶点的三角形与△AOC相似.请直接写出所有符合条件的点M坐标.
(1)、求抛物线的解析式,并直接写出点D的坐标;(2)、如图1,点P从点A出发,以每秒1个单位长度的速度沿A→B匀速运动,到达点B时停止运动.以AP为边作等边△APQ(点Q在x轴上方).设点P在运动过程中,△APQ与四边形AOCD重叠部分的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式;(3)、如图2,连接AC,在第二象限内存在点M,使得以M、O、A为顶点的三角形与△AOC相似.请直接写出所有符合条件的点M坐标.