湖北省襄阳市襄城区2017届九年级上册数学期末考试试卷

试卷更新日期：2018-01-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下面生活中的实例，不是旋转的是（　　）

A、传送带传送货物 B、螺旋桨的运动 C、风车风轮的运动 D、自行车车轮的运动

查看试题解析
2. 下列方程中,一元二次方程的个数是（）
①x²-2x-1=0；②-x²=0；③ax²+bx+c=0；④ $\frac{1}{x^{2}} + 3 x - 5 = 0$ ；⑤ $（ x - 1)^{2} + y^{2} = 2$ ；⑥ $(x - 1) (x - 3) = x^{2}$ .

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 用配方法将 $y = x^{2} - 8 x + 12$ 化成 $y = a {(x - h)}^{2} + k$ 的形式为（）

A、 $y = {(x - 4)}^{2} + 4$ B、 $y = {(x - 4)}^{2} - 4$ C、 $y = {(x - 8)}^{2} + 4$ D、 $y = {(x - 8)}^{2} - 4$

查看试题解析
4. 如图，圆锥的底面半径r为6cm，高h为8cm，则圆锥的侧面积为（）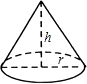

A、30πcm² B、48πcm² C、60πcm² D、80πcm²

查看试题解析
5. 不透明的袋子中装有形状、大小、质地完全相同的6个球，其中4个黑球、2个白球，从袋子中一次摸出3个球，下列事件是不可能事件的是（）

A、摸出的3个白球 B、摸出的是3个黑球 C、摸出的是2个白球、1个黑球 D、摸出的是2个黑球、1个白球

查看试题解析
6. 反比例函数 $y = - \frac{3}{x}$ 的图象在（）

A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限

查看试题解析
7. 如果两个相似三角形的面积的比是4:9,那么它们的周长的比是（）

A、4:9 B、1:9 C、1:3 D、2:3

查看试题解析
8. 如图，AB是⊙O的直径，点C为⊙O外一点，CA、CD是⊙O的切线，A，D为切点，连接BD、AD.若∠ACD=48°，则∠DBA的大小是（）

A、48° B、60° C、66° D、32°

查看试题解析
9. 下列说法正确的是（）

A、与圆有公共点的直线是圆的切线 B、过三点一定可以作一个圆 C、垂直于弦的直径一定平分这条弦 D、三角形的外心到三边的距离相等

查看试题解析
10. 二次函数的图象如图所示，对称轴为x=1，给出下列结论：①abc<0；②b²>4ac；③4a+2b+c<0；④2a+b=0..其中正确的结论有（）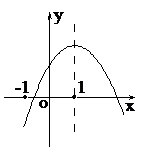

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 先后两次抛掷一枚质地均匀的硬币，落地后恰好一次正面向上，一次正面向下的概率是.

查看试题解析
12. 关于 $m$ 的方程4kx²+12x-5=0有实数根，则 $m$ 的取值范围是.

查看试题解析
13. 如图，点A是双曲线 $y = \frac{k}{x}$ 上的任意一点，过点A作AB⊥x轴于B，若△OAB的面积为8，则k=.

查看试题解析
14. 如图，在△ABC中，AC=9，AB=6，点D与点A在直线BC的同侧，且∠ACD=∠ABC，CD=3，点E是线段BC延长线上的动点，当△ABC和△DCE相似时，线段CE的长为.

查看试题解析
15. 如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=10，CD=6，则BE=.

查看试题解析
16. 二次函数 $y = \frac{1}{2} x^{2} - \frac{3}{2} x - 2$ 的图象如图所示，若线段AB在x轴上，且AB= $\frac{4}{3} \sqrt{3}$ ，以AB为边作等边△ABC，使点C落在该函数第四象限的图象上，则点C的坐标是.

查看试题解析

三、解答题

17. 先化简,再求值： $\frac{x - 1}{x} \div (2 - \frac{x^{2} + 1}{x})$ ,其中x=3.

查看试题解析
18. 如图，在Rt△ABC中，∠A=90º，AB=6，BC=10，D是AC上一点，CD=5，DE⊥BC于E.求线段DE的长.

查看试题解析
19. 如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（1，3），请解答下列问题：
①画出△ABC关于x轴对称的△A₁B₁C₁ ，并写出点B₁的坐标；②画出△ABC绕原点O逆时针旋转90°后得到的△A₂B₂C₂ ，并写出点C₂的坐标.

查看试题解析
20. 珍珍与环环两人一起做游戏，游戏规则如下：每人从1，2，3，4，5，6，7，8中任意选择一个数字，然后两人各转动一次如图所示的转盘（转盘被分为面积相等的四个扇形），两人转出的数字之和等于谁事先选择的数，谁就获胜；若两人转出的数字之和不等于她们各自选择的数，就再做一次上述游戏，直到决出胜负.若环环事先选择的数是5，用列表法或画树状图的方法，求她获胜的概率.

查看试题解析
21. 已知关于 $x$ 的一元二次方程 $x^{2} + m x + m - 2 = 0$ ．

(1)、若此方程的一个根为1，求 $m$ 的值；

(2)、求证：不论 $m$ 取何实数，此方程都有两个不相等的实数根．

查看试题解析
22. 如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD于G，OG：OC=3：5，AB=8.

(1)、求⊙O的半径；

(2)、点E为圆上一点，∠ECD=15º，将弧CE沿弦CE翻折，交CD于点F，求图中阴影部分的面积.

查看试题解析
23. 如左图，某小区的平面图是一个400×300平方米的矩形，正中央的建筑区是与整个小区长宽比例相同的矩形.如果要使四周的空地所占面积是小区面积的36%，并且南北空地与东西空地的宽度各自相同.

(1)、求该小区南北空地的宽度；

(2)、如右图，该小区在东西南三块空地上做如图所示的矩形绿化带，绿化带与建筑区之间为小区道路，小区道路宽度一致.已知东西侧绿化带完全相同，其长约为200米，南侧绿化带的长为300米，绿化面积为18000平方米，请求出小区道路的宽度.

查看试题解析
24. 如图，已知EC∥AB，∠EDA=∠ABF.

(1)、求证：四边形ABCD是平行四边形；

(2)、图中存在几对相似三角形？分别是什么？请直接写出来不必证明；

(3)、求证：OA²=OE∙OF.

查看试题解析
25. 如图，在平面直角坐标系中，抛物线 $3 x$ 与坐标轴分别交于点A，点B，点C，并且∠ACB=90º，AB=10.

(1)、求证：△OAC∽△OCB；

(2)、求该抛物线的解析式；

(3)、若点P是(2)中抛物线对称轴上的一个动点，是否存在点P使得△PAC为等腰三角形，若存在，请直接写出点P的坐标；若不存在，请说明理由.

查看试题解析