高中数学人教新课标A版必修二2.3.1直线与平面垂直的判定课时训练2
试卷更新日期：2018-01-23 类型：同步测试
一、单选题
-
1. 已知直线l垂直于直线AB和AC ， 直线m垂直于直线BC和AC ， 则直线l ， m的位置关系是（ ）
A、平行 B、异面 C、相交 D、垂直2. 已知平面α⊥平面β ， α∩β＝n ， 直线l⊂α ， 直线m⊂β ， 则下列说法正确的个数是（ ）①若l⊥n ， l⊥m ， 则l⊥β；②若l∥n ， 则l∥β；③若m⊥n ， l⊥m ， 则m⊥α.
A、0 B、1 C、2 D、33. 已知平面α⊥β ， 直线l⊂α ， 直线m⊂β ， 若l⊥m ， 则l与β的位置关系是（ ）A、l⊥β B、l∥β C、 D、以上都有可能4. PO⊥平面ABC ， O为垂足，∠ACB＝90°，∠BAC＝30°，BC＝5，PA＝PB＝PC＝10，则PO的长等于（ ）
A、5 B、 C、 D、205. 如图，在斜三棱柱ABC-A1B1C1中，∠BAC=90°，BC1⊥AC，则点C1在平面ABC上的射影H必在（ ）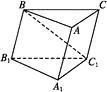
A、直线AB上 B、直线BC上 C、直线AC上 D、△ABC的内部6. 如图，在三棱锥P－ABC中，不能证明AP⊥BC的条件是（ ）
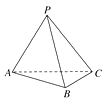A、AP⊥PB ， AP⊥PC B、AP⊥PB ， BC⊥PB C、平面BCP⊥平面PAC ， BC⊥PC D、AP⊥平面PBC二、填空题
-
7. 已知PA垂直于平行四边形ABCD所在的平面，若PC BD，则平行四边形ABCD一定是形．8. 如图，四棱锥P－ABCD的底面ABCD是边长为a的正方形，侧棱PA＝a ， ，则它的五个面中，互相垂直的平面有对．
9. 如图，在三棱锥P－ABC中，PA⊥底面ABC ， ∠BAC＝90°，F是AC的中点，E是PC上的点，且EF⊥BC ， 则 .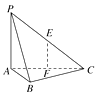
10. 如图，在直角梯形ABCD中，BC⊥DC ， AE⊥DC ， M ， N分别是AD ， BE的中点，将三角形ADE沿AE折起，则下列说法正确的是(填序号)．
①不论D折至何位置(不在平面ABC内)，都有MN∥平面DEC；②不论D折至何位置，都有MN⊥AE；③不论D折至何位置(不在平面ABC内)，都有MN∥AB；④在折起过程中，一定存在某个位置，使EC⊥AD.
三、解答题
-
11. 如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．求证：
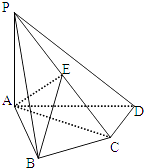
（Ⅰ）CD⊥AE；
（Ⅱ）PD⊥平面ABE．
12. 如图所示，P是四边形ABCD所在平面外的一点，四边形ABCD是∠DAB＝60°且边长为a的菱形．侧面PAD为正三角形，其所在平面垂直于底面ABCD．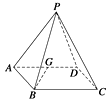
(1)、若G为AD边的中点，求证：BG⊥平面PAD；(2)、求证：AD⊥PB．
