高中数学人教新课标A版选修2-1(理科)第三章3.1.4 空间向量的正交分解及其坐标表示同步练习
试卷更新日期:2018-01-23 类型:同步测试
一、单选题
-
1. 在以下三个命题中,真命题的个数是( )
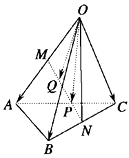
①三个非零向量a、b、c不能构成空间的一个基底,则a、b、c共面;
②若两个非零向量a、b与任何一个向量都不能构成空间的一个基底,则a、b共线;
③若a、b是两个不共线的向量,且 ,则 构成空间的一个基底.
A、0 B、1 C、2 D、32. 若 是空间的一个基底,则下列各组中不能构成空间一个基底的是( )A、a,2b,3c B、a+b,b+c,c+a C、a+2b,2b+3c,3a-9c D、a+b+c,b,c3. 已知向量 是空间的一个基底,向量 是空间的另一个基底,一向量p在基底 下的坐标为 ,则向量p在基底 下的坐标为( )A、 B、 C、 D、4. 若向量 、 、 的起点与终点M、A、B、C互不重合且无三点共线,且满足下列关系(O是空间任一点),则能使向量 、 、 成为空间一组基底的关系是( )A、 B、 C、 D、5. 已知空间四边形OABC, ,N分别是OA,BC的中点,且 , , =c,用a,b,c表示向量 为( )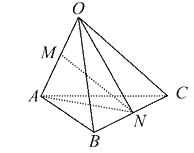 A、 B、 C、 D、6. 以下四个命题中,正确的是( )A、若 ,则P,A,B三点共线 B、向量 是空间的一个基底,则 构成空间的另一个基底 C、 D、△ABC是直角三角形的充要条件是7. 若 是空间的一个基底, , , , , ,则x,y,z的值分别为( )A、 ,-1,- B、 ,1, C、- ,1,- D、 ,1,-8. 如图,在三棱柱 ABC-A1B1C1 中, 为A1C1的中点,若=a, , ,则下列向量与 相等的是( )
A、 B、 C、 D、6. 以下四个命题中,正确的是( )A、若 ,则P,A,B三点共线 B、向量 是空间的一个基底,则 构成空间的另一个基底 C、 D、△ABC是直角三角形的充要条件是7. 若 是空间的一个基底, , , , , ,则x,y,z的值分别为( )A、 ,-1,- B、 ,1, C、- ,1,- D、 ,1,-8. 如图,在三棱柱 ABC-A1B1C1 中, 为A1C1的中点,若=a, , ,则下列向量与 相等的是( )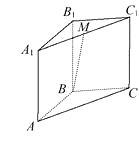 A、 B、 C、 D、9. 如图,在正方体 中,用 , , 作为基向量,则 =.
A、 B、 C、 D、9. 如图,在正方体 中,用 , , 作为基向量,则 =.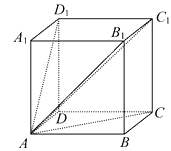
二、填空题
-
10. 已知四面体ABCD中, , ,AC,BD的中点分别为E,F,则 =.11. 在平行六面体ABCD-A1B1C1D1中,若 ,则x+y+z
三、解答题
-
12. 如图所示,在正四棱柱 中, , 分别为底面 、底面 的中心, , , 为 的中点, 在 上,且 .
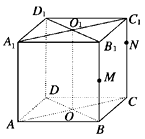 (1)、以 为原点,分别以 , 所在直线为 x 轴、 y 轴、 z 轴建立空间直角坐标系,求图中各点的坐标.(2)、以 D 为原点,分别以 , DC,DD1所在直线为 轴、 轴、 轴建立空间直角坐标系,求图中各点的坐标.
(1)、以 为原点,分别以 , 所在直线为 x 轴、 y 轴、 z 轴建立空间直角坐标系,求图中各点的坐标.(2)、以 D 为原点,分别以 , DC,DD1所在直线为 轴、 轴、 轴建立空间直角坐标系,求图中各点的坐标.