高中数学人教新课标A版选修2-1(理科)第三章3.1.1 空间向量及其加减运算,3.1.2空间向量的数乘运算同步练习
试卷更新日期:2018-01-23 类型:同步测试
一、单选题
-
1. 如图,在底面 为平行四边形的四棱柱 中,M是AC与BD的交点,若 , , ,则下列向量中与 相等的向量是 ( )
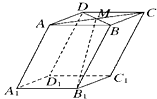 A、 B、 C、 D、2. 如图,在正方体 中,若 ,则x+y+z的值为( )
A、 B、 C、 D、2. 如图,在正方体 中,若 ,则x+y+z的值为( ) A、3 B、1 C、-1 D、-33. 在直三棱柱 中,若 , , ,则 ( )A、 B、 C、 D、4. 已知P是正六边形ABCDEF外一点,O为正六边形ABCDEF的中心,则 等于( )
A、3 B、1 C、-1 D、-33. 在直三棱柱 中,若 , , ,则 ( )A、 B、 C、 D、4. 已知P是正六边形ABCDEF外一点,O为正六边形ABCDEF的中心,则 等于( ) A、 B、 C、 D、05. 在四棱锥P-ABCD中,底面ABCD是正方形,E为PD的中点,若 ,,则 ( )
A、 B、 C、 D、05. 在四棱锥P-ABCD中,底面ABCD是正方形,E为PD的中点,若 ,,则 ( ) A、 B、 C、 D、6. 已知空间四边形 ,其对角线为 , 分别是 的中点,点 在线段 上,且使 ,用向量 表示向量 是( )
A、 B、 C、 D、6. 已知空间四边形 ,其对角线为 , 分别是 的中点,点 在线段 上,且使 ,用向量 表示向量 是( ) A、 B、 C、 D、7. 若A,B,C不共线,对于空间任意一点O都有 ,则P,A,B,C四点( )A、不共面 B、共面 C、共线 D、不共线8. 设 (其中 是两两垂直的单位向量),若 ,则实数 的值分别是( )A、1,-2,-3 B、-2,1,-3 C、-2,1,3 D、-1,2,39. 如图,在直三棱柱 中,若= , ,
A、 B、 C、 D、7. 若A,B,C不共线,对于空间任意一点O都有 ,则P,A,B,C四点( )A、不共面 B、共面 C、共线 D、不共线8. 设 (其中 是两两垂直的单位向量),若 ,则实数 的值分别是( )A、1,-2,-3 B、-2,1,-3 C、-2,1,3 D、-1,2,39. 如图,在直三棱柱 中,若= , ,C C 1 → = c → A 1 B → =  10. 已知
10. 已知A B C O 0 λ O A → + m O B → + n O C → = 0 λ + m + n
11. 在正方体A B C D − A 1 B 1 C 1 D 1 ①
( A 1 D 1 → − A 1 A → ) − A B → ( B C → + B B 1 ¯ ) − D 1 C 1 → ③
( A D → − A B ¯ ) − 2 D D 1 → ( B 1 D 1 → + A 1 A ¯ ) + D D 1 → 其中能够化简为向量
B D 1 → 二、解答题
-
12. 如图所示,在长、宽、高分别为AB=3,AD=2,
A A 1 = 1 A B C D − A 1 B 1 C 1 D 1  (1)、单位向量共有多少个?(2)、试写出模为
(1)、单位向量共有多少个?(2)、试写出模为5 (3)、试写出与A B → (4)、试写出A A 1 →

