2016年浙江省杭州市中考数学试卷
试卷更新日期:2016-10-31 类型:中考真卷
一、选择题
-
1. =( )A、2 B、3 C、4 D、52. 如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若 ,则 =( )
 A、 B、 C、 D、13. 下列选项中,如图所示的圆柱的三视图画法正确的是( )
A、 B、 C、 D、13. 下列选项中,如图所示的圆柱的三视图画法正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( )
4. 如图是某市2016年四月每日的最低气温(℃)的统计图,则在四月份每日的最低气温这组数据中,中位数和众数分别是( ) A、14℃,14℃ B、15℃,15℃ C、14℃,15℃ D、15℃,14℃5. 下列各式变形中,正确的是( )A、x2•x3=x6 B、 =|x| C、(x2﹣ )÷x=x﹣1 D、x2﹣x+1=(x﹣ )2+6. 已知甲煤场有煤518吨,乙煤场有煤106吨,为了使甲煤场存煤是乙煤场的2倍,需要从甲煤场运煤到乙煤场,设从甲煤场运煤x吨到乙煤场,则可列方程为( )A、518=2(106+x) B、518﹣x=2×106 C、518﹣x=2(106+x) D、518+x=2(106﹣x)7. 设函数y= (k≠0,x>0)的图象如图所示,若z= ,则z关于x的函数图象可能为( )
A、14℃,14℃ B、15℃,15℃ C、14℃,15℃ D、15℃,14℃5. 下列各式变形中,正确的是( )A、x2•x3=x6 B、 =|x| C、(x2﹣ )÷x=x﹣1 D、x2﹣x+1=(x﹣ )2+6. 已知甲煤场有煤518吨,乙煤场有煤106吨,为了使甲煤场存煤是乙煤场的2倍,需要从甲煤场运煤到乙煤场,设从甲煤场运煤x吨到乙煤场,则可列方程为( )A、518=2(106+x) B、518﹣x=2×106 C、518﹣x=2(106+x) D、518+x=2(106﹣x)7. 设函数y= (k≠0,x>0)的图象如图所示,若z= ,则z关于x的函数图象可能为( )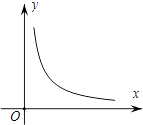 A、
A、 B、
B、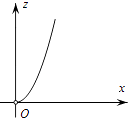 C、
C、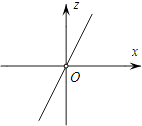 D、
D、 8. 如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )
8. 如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( ) A、DE=EB B、 DE=EB C、 DE=DO D、DE=OB9. 已知直角三角形纸片的两条直角边长分别为m和n(m<n),过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则( )A、m2+2mn+n2=0 B、m2﹣2mn+n2=0 C、m2+2mn﹣n2=0 D、m2﹣2mn﹣n2=010. 设a,b是实数,定义@的一种运算如下:a@b=(a+b)2﹣(a﹣b)2 , 则下列结论:
A、DE=EB B、 DE=EB C、 DE=DO D、DE=OB9. 已知直角三角形纸片的两条直角边长分别为m和n(m<n),过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则( )A、m2+2mn+n2=0 B、m2﹣2mn+n2=0 C、m2+2mn﹣n2=0 D、m2﹣2mn﹣n2=010. 设a,b是实数,定义@的一种运算如下:a@b=(a+b)2﹣(a﹣b)2 , 则下列结论:①若a@b=0,则a=0或b=0
②a@(b+c)=a@b+a@c
③不存在实数a,b,满足a@b=a2+5b2
④设a,b是矩形的长和宽,若矩形的周长固定,则当a=b时,a@b最大.
其中正确的是( )
A、②③④ B、①③④ C、①②④ D、①②③二、填空题
-
11. tan60°= .12. 已知一包糖果共有5种颜色(糖果只有颜色差别),如图是这包糖果分布百分比的统计图,在这包糖果中任意取一粒,则取出糖果的颜色为绿色或棕色的概率是 .
 13. 若整式x2+ky2(k为不等于零的常数)能在有理数范围内因式分解,则k的值可以是(写出一个即可).14. 在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为 .15. 在平面直角坐标系中,已知A(2,3),B(0,1),C(3,1),若线段AC与BD互相平分,则点D关于坐标原点的对称点的坐标为 .16. 已知关于x的方程 =m的解满足 (0<n<3),若y>1,则m的取值范围是 .
13. 若整式x2+ky2(k为不等于零的常数)能在有理数范围内因式分解,则k的值可以是(写出一个即可).14. 在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为 .15. 在平面直角坐标系中,已知A(2,3),B(0,1),C(3,1),若线段AC与BD互相平分,则点D关于坐标原点的对称点的坐标为 .16. 已知关于x的方程 =m的解满足 (0<n<3),若y>1,则m的取值范围是 .三、解答题
-
17. 计算6÷(﹣ ),方方同学的计算过程如下,原式=6 +6 =﹣12+18=6.请你判断方方的计算过程是否正确,若不正确,请你写出正确的计算过程.18. 某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:
 (1)、若第一季度的汽车销售量为2100辆,求该季的汽车产量;(2)、圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么?19. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且 .
(1)、若第一季度的汽车销售量为2100辆,求该季的汽车产量;(2)、圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么?19. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且 .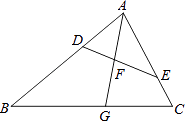 (1)、求证:△ADF∽△ACG;(2)、若 ,求 的值.20. 把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤4).(1)、当t=3时,求足球距离地面的高度;(2)、当足球距离地面的高度为10米时,求t;(3)、若存在实数t1 , t2(t1≠t2)当t=t1或t2时,足球距离地面的高度都为m(米),求m的取值范围.21. 如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)、求证:△ADF∽△ACG;(2)、若 ,求 的值.20. 把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤4).(1)、当t=3时,求足球距离地面的高度;(2)、当足球距离地面的高度为10米时,求t;(3)、若存在实数t1 , t2(t1≠t2)当t=t1或t2时,足球距离地面的高度都为m(米),求m的取值范围.21. 如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H. (1)、求sin∠EAC的值.(2)、求线段AH的长.22. 已知函数y1=ax2+bx,y2=ax+b(ab≠0).在同一平面直角坐标系中.(1)、若函数y1的图象过点(﹣1,0),函数y2的图象过点(1,2),求a,b的值.(2)、若函数y2的图象经过y1的顶点.
(1)、求sin∠EAC的值.(2)、求线段AH的长.22. 已知函数y1=ax2+bx,y2=ax+b(ab≠0).在同一平面直角坐标系中.(1)、若函数y1的图象过点(﹣1,0),函数y2的图象过点(1,2),求a,b的值.(2)、若函数y2的图象经过y1的顶点.①求证:2a+b=0;
②当1<x< 时,比较y1 , y2的大小.
23.在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时:
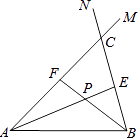 (1)、点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;(2)、设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ,求AQ的长.
(1)、点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;(2)、设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ,求AQ的长.