江苏省盐城市阜宁县2017-2018学年九年级上学期数学期末考试试卷

试卷更新日期：2018-01-17 类型：期末考试

进入出卷网下载

一、选择题

1. 下列统计量中，能够刻画一组数据的离散程度的是（）

A、方差或标准差 B、平均数或中位数 C、众数或频率 D、频数或众数

查看试题解析
2. 在比例尺为1：38 000的城市交通地图上，某条道路的长为5 cm，则它的实际长度为（）

A、0.19 km B、1.9 km C、19 km D、190 km

查看试题解析
3. 给出下列各组线段，其中成比例线段是（）

A、 $a = 2 c m ， b = 4 c m ， c = 6 c m ， d = 8 c m$ B、 $a = \frac{1}{2} c m ， b = \frac{1}{4} c m ， c = \frac{1}{6} c m ， d = \frac{1}{8} c m$ C、 $a = \sqrt{2} c m ， b = \sqrt{3} c m ， c = \sqrt{10} c m ， d = 2 \sqrt{5} c m$ D、 $a = 2 c m ， b = \sqrt{5} c m ， c = 2 \sqrt{3} c m ， d = \sqrt{15} c m$

查看试题解析
4. 在Rt△ABC中，∠C=90°， $\sin A = \frac{3}{5}$ ,则 $\cos B$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
5. 已知正三角形的边长为12，则这个正三角形外接圆的半径是（）

A、 $2 \sqrt{3}$ B、 $\sqrt{3}$ C、 $3 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
6. 如图，点A、C、B在⊙O上，已知∠AOB=∠ACB=α．则α的值为（）

A、135° B、120° C、110° D、100°

查看试题解析
7. 抛物线 $y = a x^{2} + b x + c$ 上部分点坐标如表所示，下列说法错误的是（）
x
…
－3
－2
－1
0
1
…
y
…
－6
0
4
6
6
…

A、抛物线与y轴的交点为(0，6) B、抛物线的对称轴是在y轴的右侧； C、抛物线一定经过点(3 ， 0) D、在对称轴左侧， y随x增大而减小．

查看试题解析
8. 如图，以点O为圆心的两个圆中，大圆的弦AB切小圆于点C，OA交小圆于点D，若 $O D = 2 ， \tan A = \frac{1}{2}$ ，则AB长为（）

A、4 B、 $2 \sqrt{3}$ C、8 D、 $4 \sqrt{3}$

查看试题解析

二、填空题

9. 若 $\sin α = \frac{\sqrt{3}}{2}$ ，则锐角α= ．

查看试题解析
10. 已知 $3, a, 4, b, 5$ 这五个数据，其中 $a$ 、 $b$ 是方程 $x^{2} - 3 x + 2 = 0$ 的两个根，则这五个数据的极差是．

查看试题解析
11. 若 $D ， E ， F$ 分别为 $Δ A B C$ 各边的中点，且 $Δ D E F$ 的周长为9，则 $Δ A B C$ 的周长为

查看试题解析
12. 某种品牌的手机经过十一、十二月份连续两次降价，每部售价由3200元降到了2500元．设平均每月降价的百分率为x，根据题意列出的方程是．

查看试题解析
13. 甲、乙、丙3名学生随机排成一排拍照，其中甲排在中间的概率是.

查看试题解析
14. 若关于x的方程x²＋2x＋k＝0有两个不相等的实数根，则k的取值范围是．

查看试题解析
15. 已知圆锥的底面半径为3cm，其母线长为5cm，则它的侧面积为 ${cm}^{2}$ ．

查看试题解析
16. 如图∠DAB＝∠CAE，请补充一个条件：，使△ABC∽△ADE．

查看试题解析
17. 在△ABC中，（tanC-1）² +∣ $\sqrt{3}$ -2cosB∣=0，则∠A=

查看试题解析
18. 如图，在平面直角坐标系中，已知点A、B的坐标分别为（8，0）、（0，2 $\sqrt{3}$ ），C是AB的中点，过点C作y轴的垂线，垂足为D，动点P从点D出发，沿DC向点C匀速运动，过点P作x轴的垂线，垂足为E，连接BP、EC．当BP所在直线与EC所在直线垂直时，点P的坐标为

查看试题解析

三、解答题

19.

(1)、计算： $2 \sin 30^{\circ} + 3 \cos 60^{\circ} - 4 \tan 45^{\circ}$

(2)、解方程： $x^{2} - 2 x - 1 = 0$

查看试题解析
20. 某工厂甲、乙两名工人参加操作技能培训．现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次，记录如下：
甲
95
82
88
81
93
79
84
78
乙
83
92
80
95
90
80
85
75

(1)、请你计算这两组数据的平均数、中位数；

(2)、现要从中选派一人参加操作技能比赛，从统计学的角度考虑，你认为选派哪名工人参加合适？请说明理由．

查看试题解析
21. 甲、乙、丙3名学生各自随机选择到A、B 2个书店购书.

(1)、求甲、乙2名学生在不同书店购书的概率；

(2)、求甲、乙、丙3名学生在同一书店购书的概率.

查看试题解析
22. 如图，在矩形ABCD中，AB=6，AD=12，点E在AD边上，且 AE=8，EF⊥BE交CD于点 F .

(1)、求证： $△ A B E ∽ △ D E F$ .

(2)、求CF的长.

查看试题解析
23. 如图，ABCD是围墙，AB∥CD，∠ABC=120°，一根6m长的绳子，一端拴在围墙一角的柱子上（B处），另一端拴着一只羊（E处）．

(1)、请在图中画出羊活动的区域．

(2)、求出羊活动区域的面积．(保留π)

查看试题解析
24. 如图，在△ABD和△ACE中，AB=AD，AC=AE，∠BAD=∠CAE，连接BC、DE相交于点F，BC与AD相交于点G．

(1)、试判断线段BC、DE的数量关系，并说明理由；

(2)、若BC平分∠ABD，求证线段FD是线段FG 和 FB的比例中项.

查看试题解析
25. 大海中某小岛周围10 $k m$ 范围内有暗礁，一海轮在该岛的南偏西 $60^{\circ}$ 方向的某处，由西向东行驶了 $20 k m$ 后到达该岛的南偏西 $30^{\circ}$ 方向的另一处，如果该海轮继续向东行驶，会有触礁的危险吗？（ $\sqrt{3}$ ≈1.732）．

查看试题解析
26. 如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点D恰好为BC的中点，过点D作⊙O的切线交AC边于点F.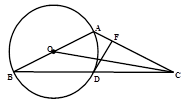

(1)、求证：DF⊥AC；

(2)、若∠ABC=30°，求tan∠BCO的值.

查看试题解析
27. 在Rt△ABC中，∠C=90°，P是BC边上不同于B、C的一动点，过P作PQ⊥AB，垂足为Q，连接AP．

(1)、试说明不论点P在BC边上何处时，都有△PBQ与△ABC相似；

(2)、若Rt△AQP≌Rt△ACP≌Rt△BQP，求 $\tan B$ 的值；

(3)、已知AC=3，BC=4，当BP为何值时，△AQP面积最大，并求出最大值.

查看试题解析
28. 如图，已知抛物线y＝ax²＋bx＋c与x轴交于A、B两点，与y轴交于点C， D为OC的中点，直线AD交抛物线于点E（2，6），且△ABE与△ABC的面积之比为3∶2．

(1)、求这条抛物线对应的函数关系式；

(2)、连结BD，试判断BD与AD的位置关系，并说明理由；

(3)、连结BC交直线AD于点M，在直线AD上，是否存在这样的点N（不与点M重合），使得以A、B、N为顶点的三角形与△ABM相似？若存在，请求出点N的坐标；若不存在，请说明理由．

查看试题解析

x	…	－3	－2	－1	0	1	…
y	…	－6	0	4	6	6	…

甲	95	82	88	81	93	79	84	78
乙	83	92	80	95	90	80	85	75