江苏省盐城市阜宁县2017-2018学年八年级上学期数学期末考试试卷

试卷更新日期：2018-01-17 类型：期末考试

进入 出卷网 下载

一、选择题

  • 1. 在下列黑体大写英文字母中，不是轴对称图形的是（   ）
    A、E B、M C、N D、H

    查看试题解析

  • 2. 下列各点中，位于第四象限的点是（   ）
    A、(3，4) B、(－3，4) C、(3，－4) D、(－3，－4)

    查看试题解析

  • 3. 下列条件中，不能判定两个三角形全等的是（   ）
    A、两边一角对应相等 B、两角一边对应相等 C、直角边和一个锐角对应相等 D、三边对应相等

    查看试题解析

  • 4. 下列语句中，正确的是（   ）
    A、正整数、负整数统称整数 B、正数、0、负数统称为有理数 C、开方开不尽的数和 π 统称无理数 D、有理数、 无理数统称实数

    查看试题解析

  • 5. 下列各组数中，是勾股数的（   ）
    A、12，15，18 B、11，60，61 C、15，16，17 D、12，35，36

    查看试题解析

  • 6. 一次函数 y=−2x+3 的图象不经过的象限是（   ）
    A、第一象限 B、第二象限 C、第三象限 D、第四象限

    查看试题解析

  • 7. 要使 x−5 有意义， x 的取值范围是（   ）
    A、x≥5 B、x≤5 C、x>5 D、x<5

    查看试题解析

  • 8. 已知一个直角三角形的两直角边长分别为3和4，则斜边长是（   ）
    A、5 B、14 C、7 D、7 或5

    查看试题解析

二、填空题

  • 9. 化简 12=   ．

    查看试题解析

  • 10. 如果直角三角形斜边上的中线长为6cm，那么这个直角三角形的斜边长为cm．

    查看试题解析

  • 11. 点P (m,m+3) 在平面直角坐标系的y轴上，则点P的坐标是 ．

    查看试题解析

  • 12. 若正比例函数的图象过点A(3，－5)，则该正比例函数的表达式为 ．

    查看试题解析

  • 13. 由四舍五入法得到的近似数1.59精确程度为 ．

    查看试题解析

  • 14. 在 ΔABC 中， AB＝AC＝17cm ， BC=16cm ，AD是角平分线，则 ΔABC 的面积为cm2 ．

    查看试题解析

  • 15. 若 a2=−a ，则a应满足的条件是 ．

    查看试题解析

三、解答题

  • 16. 计算                       
    (1)、18a⋅2a(a≥0)                              
    (2)、412÷214  
    (3)、12+18−8−32                        
    (4)、(3+10)(2−5)  

    查看试题解析

  • 17. 如图，在 ΔABC 中，AD是高，E、F分别是AB、AC的中点，

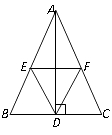    (1)、AB＝10，AC＝8，求四边形AEDF的周长；
    (2)、EF与AD有怎样的位置关系，证明你的结论．

    查看试题解析

  • 18. 计算图中四边形ABCD的面积．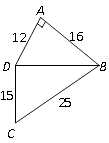

    查看试题解析

  • 19. 往一个长25m，宽11m的长方体游泳池注水，水位每小时上升0.32m，
    (1)、写出游泳池水深d(m)与注水时间x(h)的函数表达式；
    (2)、如果x(h)共注水y(m3)，求y与x的函数表达式；
    (3)、如果水深1.6m时即可开放使用，那么需往游泳池注水几小时？注水多少(单位：m3)？

    查看试题解析

  • 20. 某长途汽车客运公司规定旅客可以免费携带一定质量的行李，当行李的质量超过规定时，需付的行李费y(元)与行李质量x(kg)之间的函数表达式为 y=kx+b ，这个函数的图象如图所示，求：

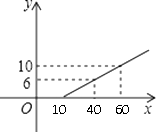    (1)、k和b的值；
    (2)、旅客最多可免费携带行李的质量；
    (3)、行李费为4~15元时，旅客携带行李的质量为多少？

    查看试题解析

  • 21. 已知 a−5−2+b−5+2=0 求 a2+b2+7 的值。

    查看试题解析

  • 22. 如图。在每个小正方形的边长均为1个单位长度的方格纸中，有线段AB和直线MN，点A、B、M、N均在小正方形的顶点上．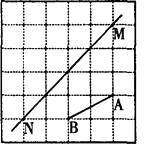

    (1)、在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上)，使四边形ABCD是以直线MN为对称轴的轴对称图形，点A的对称点为点D，点B的对称点为点C；
    (2)、请直接写出四边形ABCD的周长．

    查看试题解析

  • 23. 如图，有两颗树，一颗高10米，另一颗高4米，两树相距8米．一只鸟从一颗树的树梢飞到另一颗树的树梢，问小鸟至少飞行几米？

    查看试题解析

  • 24. 如图，A（0，1），M（3，2），N（4，4）.动点P从点A出发，沿轴以每秒1个单位长的速度向上移动，且过点P的直线l：y＝－x+b也随之移动，设移动时间为t秒.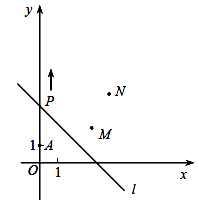

    (1)、当t＝3时，求l的解析式；
    (2)、若点M，N位于l的异侧，确定t的取值范围；
    (3)、直接写出t为何值时，点M关于l的对称点落在坐标轴上.

    查看试题解析

  • 25. 如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站的路程y1 ， y2（千米）与行驶时间x（小时）之间的函数关系图象．

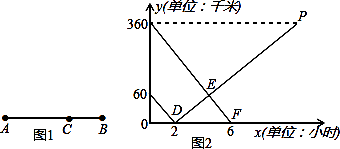    (1)、填空：A，B两地相距千米；
    (2)、求两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式；
    (3)、客、货两车何时相遇？相遇处离C站的路程是多少千米？

    查看试题解析