湖南省醴陵市2016-2017年学年七年级上学期数学期末考试试卷

试卷更新日期：2018-01-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是品牌汽车的标识，在这些汽车标识中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $x^{8} \div x^{2} = x^{4}$ B、 $x^{8} \cdot x^{2} = x^{16}$ C、 ${(x^{2} \cdot x^{3})}^{2} = x^{10}$ D、 ${(- x^{5})}^{4} = - x^{20}$

查看试题解析
3. 下面四个图形中关于∠1与∠2位置关系表述错误的是（）。

A、互为对顶角 B、互为邻补角 C、互为内错角 D、互为同位角

查看试题解析
4. 在数据1，3，5，5中，中位数是（）

A、3 B、4 C、5 D、7

查看试题解析
5. 把x²y﹣2y²x+y³分解因式正确的是（）

A、y（x﹣y）² B、x²y﹣y²（2x﹣y） C、y（x²﹣2xy+y²） D、y（x+y）²

查看试题解析
6. 已知 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ 是方程2mx﹣y=10的解，则m的值为（）

A、2 B、4 C、6 D、10

查看试题解析
7. 下列说法中正确的是（）

A、旋转一定会改变图形的形状和大小 B、两条直线被第三条直线所截，同位角相等 C、在同一平面内，过一点有且只有一条直线与已知直线垂直 D、相等的角是对顶角

查看试题解析
8. 如图，可以判定AD//BC的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、 $∠ D A B + ∠ A B C = 180 °$ D、 $∠ A B C + ∠ B C D = 180 °$

查看试题解析
9. 如图，将△ABC绕着点C按顺时针方向旋转20°，B点落在 $B^{'}$ 位置，A点落在 $A^{'}$ 位置，若 $A C ⊥ A^{'} B^{'}$ ，则 $∠ B A C$ 的度数是（）

A、80° B、70° C、60° D、50°

查看试题解析
10. 如图所示，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（）

A、（a﹣b）²=a²﹣2ab+b² B、（a+b）²=a²+2ab+b² C、a²﹣b²=（a+b）（a﹣b） D、a²+ab=a（a+b）

查看试题解析

二、填空题

11. 计算： $2 x \cdot (x^{2} + y^{2})$ =

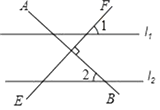
查看试题解析
12. 因式分解：6（x﹣3）+x（3﹣x）= ．

查看试题解析
13. 已知多项式 $x^{2} - m x + \frac{1}{4}$ 是完全平方式，则m的值为

查看试题解析
14. 如图，直线l₁∥l₂ ， AB⊥EF，∠1=40°，那么∠2= ．

查看试题解析
15. 已知a+b=2，ab=1，则a² + b²＝．

查看试题解析
16. 若x，y满足方程（x+y﹣a）²+|2x-y﹣b|=0，则x-2y=(用含a、b的代数式表示)．

查看试题解析

三、解答题

17. 先化简，再求值： $(3 x + 2) (3 x - 2) - {(3 x - 1)}^{2}$ ，其中 $x = - \frac{1}{2}$ .

查看试题解析
18. 解方程组： ${\begin{matrix} 2 x - y = 5 \\ 3 x + 2 y = 4 \end{matrix}$

查看试题解析
19. 如图，EF∥AD，∠1=∠2， ∠BAC=70°，将求∠AGD的过程填空完整。
解：∵EF∥AD
∴∠2=（）
又∵∠1=∠2
∴∠1=∠3（）
∴AB∥（）
∵∠BAC+=180°（）
∵∠BAC=70° ∴∠AGD=。

查看试题解析
20. 如图，在正方形网格中，有格点三角形ABC（顶点都是格点）和直线MN.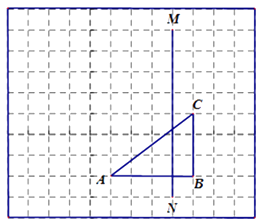
①画出三角形ABC关于直线MN对称的三角形 $A_{1} B_{1} C_{1}$
②将三角形ABC绕点A按逆时针方向旋转90°得到三角形 $A B_{2} C_{2}$ ，在正方形网格中画出三角形 $A B_{2} C_{2}$ 。（不要求写作法）

查看试题解析
21. 甲，乙两支仪仗队队员的身高（单位：cm）如下：
甲队：178，177，179，178，177，178，177，179，178，179；
乙队：178，179，176，178，180，178，176，178，177，180；

(1)、将下表填完整：
身高
176
177
178
179
180
甲队（人数）
3
4
乙队（人数）
2
1
1

(2)、甲队队员身高的平均数为cm，乙队队员身高的平均数为cm；

(3)、你认为哪支仪仗队更为整齐？简要说明理由．

查看试题解析
22. 为了满足广大市民对新能源汽车的需求，我市某汽车销售公司决定到某汽车制造厂采购A，B两种型号的新能源轿车。若用300万元，则可购进A型轿车10辆，B型轿车15辆；若用320万元，则可购进A型轿车8辆，B型轿车20辆，求A，B两种型号的新能源轿车的单价分别为多少万元？

查看试题解析
23. 综合题：探索发现

(1)、分解因式：①（1＋x）＋x(1＋x)＝（）（）＝（）²
②（1＋x）＋x(1＋x) ＋ x(1＋x)²＝
③（1＋x）＋x(1＋x) ＋ x(1＋x)² ＋ x(1＋x)³＝

(2)、根据（1）的规律，直接写出多项式：(1＋x) ＋x(1＋x) ＋ x(1＋x)²＋…＋ x(1＋x)²⁰¹⁷分解因式的结果：。

(3)、变式： $(1 - x) (1 + x) (1 + x^{2}) (1 + x^{4}) \cdot \cdot \cdot (1 + x^{2 n})$ = .

查看试题解析
24. 如图，点E在直线BH、DC之间，点A为BH上一点，且AE⊥CE， $∠ D C E - ∠ H A E = 90 °$ .

(1)、求证：BH∥CD；

(2)、如图：直线AF交DC于F，AM平分∠EAF，AN平分∠BAE. 试探究∠MAN，∠AFG的数量关系.

查看试题解析

身高	176	177	178	179	180
甲队（人数）		3	4
乙队（人数）	2	1		1