北京市西城区2016-2017学年七年级上学期数学期末考试试卷
试卷更新日期:2018-01-17 类型:期末考试
一、单选题
-
1. 规定海平面的海拔高度为0米,珠穆朗玛峰高于海平面8844.43米,其海拔高度记作+8844.43米,那么吐鲁番盆地低于海平面155米,则其海拔高度记作( )
A、+155米 B、-155米 C、+8689.43米 D、-8689.43米2. 北京新机场是京津冀协同发展中的重点工程。2016年,北京新机场主体工程已开工建设,其中T1航站区建筑群总面积为1 430 000平方米,计划于2019年交付使用。将1 430 000用科学记数法表示为( )
A、1430×103 B、143×104 C、14.3×105 D、1.43×1063. 下列运算中,正确的是( )A、4x+3y=7xy B、3x2+2=5x2 C、6xy-4xy=2xy D、5x2-x2=44. 下列方程中,解为x=4的方程是( ).A、x-1=4 B、4x=1 C、4x-1=3x+3 D、2(x-1)=15. 如图所示,用量角器度量一些角的度数。下列结论中正确的是( ) A、∠BOC=60° B、∠COD=150° C、∠AOC与∠BOD的大小相等 D、∠AOC与∠BOD互余6. 已知a2+3a=1,则代数式2a2+6a-1的值为( )A、1 B、2 C、3 D、07. 如图,点C在线段AB上,D是线段AC的中点。若CB=2,CD=3CB,则线段AB的长为( )
A、∠BOC=60° B、∠COD=150° C、∠AOC与∠BOD的大小相等 D、∠AOC与∠BOD互余6. 已知a2+3a=1,则代数式2a2+6a-1的值为( )A、1 B、2 C、3 D、07. 如图,点C在线段AB上,D是线段AC的中点。若CB=2,CD=3CB,则线段AB的长为( ) A、6 B、10 C、14 D、188. 有理数a,b在数轴上的对应点的位置如图所示,则下列式子中正确的是( )
A、6 B、10 C、14 D、188. 有理数a,b在数轴上的对应点的位置如图所示,则下列式子中正确的是( )
①b<0<a;②|b|<|a|;③ab>0;④a-b>a+b。
A、①② B、①④ C、②③ D、③④9. 甲、乙两人同时开始采摘樱桃,甲平均每小时采摘8公斤樱桃,乙平均每小时采摘7公斤樱桃。采摘同时结束后,甲从他采摘的樱桃中取出1公斤给了乙,这时两人的樱桃一样多。他们采摘樱桃用了多长时间?设他们采摘了x小时,则下面所列方程中正确的是( )A、8x-1=7x+1 B、8x-1=7x C、8x+l=7x D、8x+l=7x-110. 下列四张正方形硬纸片,分别将阴影部分剪去后,再沿虚线折叠,其中可以围成一个封闭长方体包装盒的是( )
A、 B、
B、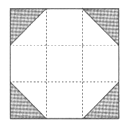 C、
C、 D、
D、
二、填空题
-
11. |-2017|=。12. 用四舍五入法对8.637取近似数并精确到0.01,得到的值是。
13. 角度换算:45.6°=°'。14. 写出单项式-3a2b的一个同类项:。
15. 对于有理数m,n,我们规定m n=mn-n,例如3 5=3×5-5=10,则(-6) 4=。
16. 下面的框图表示解方程3x-7(x-1)=3-2(x+3)的流程,其中A代表的步骤是 , 步骤A对方程进行变形的依据是。 17. “x与y的积”用代数式表示为xy,老师提出单项式“xy”可以解释为:一件商品的单价为x元,则购买y件此商品共需要花费xy元。
17. “x与y的积”用代数式表示为xy,老师提出单项式“xy”可以解释为:一件商品的单价为x元,则购买y件此商品共需要花费xy元。
(1)、小晨对“xy”也赋予了一个含义:圆柱的底面积为x平方米,高为y米,则它的为xy立方米;
(2)、请你参照他们的说法对“xy”再赋予一个含义:。
18. 观察下面的图形(每个正方形的边长均为1)和相应的等式,探究其中的规律:①

 1× =1-
1× =1- ②

 2× =2-
2× =2- ③

 3× =3-
3× =3- ……
(1)、在下面给出的四个正方形中画出第四个图形,并在右边写出与之对应的等式;
 ;(2)、猜想并写出与第n个图形相对应的等式:。19. 如图,点C在射线OA上,CE平分∠ACD. OF平分∠COB并与射线CD交于点F。
;(2)、猜想并写出与第n个图形相对应的等式:。19. 如图,点C在射线OA上,CE平分∠ACD. OF平分∠COB并与射线CD交于点F。 (1)、依题意补全图形;(2)、若∠COB+∠OCD=180°,求证:∠ACE=∠COF。
(1)、依题意补全图形;(2)、若∠COB+∠OCD=180°,求证:∠ACE=∠COF。请将下面的证明过程补充完整。
证明:∵CE平分∠ACD,OF平分∠COB,
∴∠ACE= , ∠COF= ∠COB。
(理由: )
∵点C在射线OA上,
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°,
∴∠ACD=∠。
(理由: )
∴∠ACE=∠COF。
20. 一个二元码是由0和1组成的数字串x1x2…xn(n为正整数),其中xk(k=1,2,…,n)称为第k位码元,如:二元码01101的第1位码元为0,第5位码元为1。(1)、二元码100100的第4位码元为;
(2)、二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)。已知某种二元码x1x2…x7的码元满足如下校验方程组:其中运算 定义为:0 0=0,1 1=0,0 1=1,1 0=1。
①计算:0 1 1 0=;
②现已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了0101101,那么利用上述校验方程组可判定k等于。
三、解答题
-
21. 13+(-5)-(-21)-19
22. (-1 )×(-9)÷(- )
23. 36×( - - )24. (-2)3×[-7+(3-1.2× )]
25. 求3(4x2y-2y2)-(10x2y-6y2)的值,其中x=3,y=-2。
26. 解方程: +1= .
27. 解方程组:
28. 自2014年12月28日北京公交地铁调价以来,人们的出行成本发生了较大的变化. 小林根据新闻,将地铁和公交车的票价绘制成了如下两个表格。(说明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他类似)
北京地铁新票价
里程范围
对应票价
0~6公里
3元
6~12公里
4元
12~22公里
5元
22~32公里
6元
32公里以上
每增加1元可再乘坐20公里
*持市政交通一卡通花费累计满一定金额后可打折

北京公交车新票价
里程范围
对应票价
0~10公里
2元
10~15公里
3元
15~20公里
4元
20公里以上
每增加1元可再乘坐5公里
*持市政交通一卡通刷卡,普通卡打5折,
学生卡打2.5折
根据以上信息回答下列问题:
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣。
(1)、如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费元;(2)、如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交元;(3)、小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?29. A,B两点在数轴上的位置如图所示,其中点A对应的有理数为-4,且AB=10。动点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒(t>0)。 (1)、当t=1时,AP的长为 , 点P表示的有理数为;
(1)、当t=1时,AP的长为 , 点P表示的有理数为;
(2)、当PB=2时,求t的值;(3)、M为线段AP的中点,N为线段PB的中点. 在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长。
30. 在茫茫宇宙中,存在着一种神秘的天体,任何物质经过它的附近都会被它吸引进去,再也不能出来,这就是黑洞。在数学中也有这种神秘的黑洞现象,被称为“西西弗斯串”。“西西弗斯串”是指任意设定一个数字串,数出其中所含偶数数字的个数、奇数数字的个数、数字的总个数,将它们按照“偶—奇—总”的顺序排列成新的数字串,再将新的数字串按照上述规则重复进行下去,……最终总能得到一个不再变化的数字串。(1)、例如,11位的数字串46818957892,其中偶数数字有6个,奇数数字有5个,数字总个数是11个,按上述规则操作得到新的数字串6511;将所得4位数字串6511再次按规则进行操作可得到新的数字串;若一直按规则重复进行操作,最终得到的数字;(2)、请你再任意写出一个数字串,按照上述规则重复进行操作,写出操作过程中的结果,并确定最终得到的数字串。31. 阅读下列材料:《张丘建算经》是一部数学问题集,其内容、范围与《九章算术》相仿。其中提出并解决了一个在数学史上非常著名的不定方程问题,通常称为“百鸡问题”:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。凡百钱买鸡百只,问鸡翁、母、雏各几何。”

译文:公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱。现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?
结合你学过的知识,解决下列问题:
(1)、若设公鸡有x只,母鸡有y只,①则小鸡有只,买小鸡一共花费文钱;(用含x,y的式子表示)
②根据题意列出一个含有x,y的方程: ;
(2)、若对“百鸡问题”增加一个条件:公鸡数量是母鸡数量的3倍,求此时公鸡、母鸡、小鸡各有多少只?(3)、除了问题(2)中的解之外,请你再直接写出两组符合“百鸡问题”的解。