北京市延庆区2016届九年级上册数学期末考试试卷
试卷更新日期:2018-01-15 类型:期末考试
一、单选题
-
1. ⊙O的半径为R,点P到圆心O的距离为d,并且d ≥ R,则P点( )A、在⊙O内或圆周上 B、在⊙O外 C、在圆周上 D、在⊙O外或圆周上2. 把10cm长的线段进行黄金分割,则较长线段的长(≈2.236,精确到0.01)是( )A、3.09cm B、3.82cm C、6.18cm D、7.00cm3. 如图,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,若AD=4,DB=2,则AE︰EC的值为( )
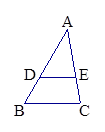 A、0.5 B、 2 C、 D、4. 反比例函数 的图象如图所示,则K的值可能是( )
A、0.5 B、 2 C、 D、4. 反比例函数 的图象如图所示,则K的值可能是( )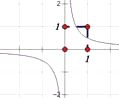 A、 B、1 C、2 D、-15. 在Rt△ 中,∠C=90°,BC=1,那么AB的长为( )
A、 B、1 C、2 D、-15. 在Rt△ 中,∠C=90°,BC=1,那么AB的长为( )
A、 B、 C、 D、6. 如图,正三角形内接于⊙O,动点P在圆周的劣弧 上,且不与A,B重合,则∠BPC等于( )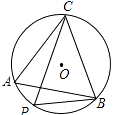 A、 B、 C、 D、7. 抛物线y= x2的图象向左平移2个单位,在向下平移1个单位,得到的函数表达式为( )A、y = x2+ 2x + 1 B、y = x2 + 2x - 2 C、y = x2 - 2x - 1 D、y = x2 - 2x + 18. 已知二次函数 的图象如图所示,有下列5个结论:① ;② ;③ ;④ ; ⑤ ,( 的实数)其中正确的结论有( )
A、 B、 C、 D、7. 抛物线y= x2的图象向左平移2个单位,在向下平移1个单位,得到的函数表达式为( )A、y = x2+ 2x + 1 B、y = x2 + 2x - 2 C、y = x2 - 2x - 1 D、y = x2 - 2x + 18. 已知二次函数 的图象如图所示,有下列5个结论:① ;② ;③ ;④ ; ⑤ ,( 的实数)其中正确的结论有( )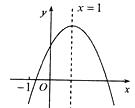 A、2个 B、3个 C、4个 D、5个9. 如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE2=AB CF;③CF= FD; ④△ABE∽△AEF.其中正确的有( )
A、2个 B、3个 C、4个 D、5个9. 如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE2=AB CF;③CF= FD; ④△ABE∽△AEF.其中正确的有( ) A、1个 B、2个 C、3个 D、4个10. 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC边上一个动点,EF∥BC,交AB 于点E,交AC于点F,设E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致为( )
A、1个 B、2个 C、3个 D、4个10. 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC边上一个动点,EF∥BC,交AB 于点E,交AC于点F,设E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致为( )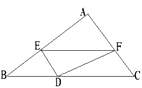 A、
A、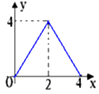 B、
B、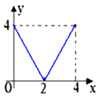 C、
C、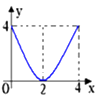 D、
D、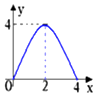
二、填空题
-
11. 若 ,则 = .12. 两个相似多边形相似比为1:2,且它们的周长和为90,则这两个相似多边形的周长分别是 .
13. 已知扇形的面积为15πcm2,半径长为5cm ,则扇形周长为cm.14. 在Rt△ABC中,∠C=90°,AC=4,BC=3,则以2.5为半径的⊙C与直线AB的位置关系是 .
15. 请选择一组你喜欢的a,b,c的值,使二次函数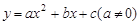 的图象同时满足下列条件:①开口向下,②当 时, 随 的增大而增大;当 时,y随x的增大而减小.这样的二次函数的表达式可以是
的图象同时满足下列条件:①开口向下,②当 时, 随 的增大而增大;当 时,y随x的增大而减小.这样的二次函数的表达式可以是
16. 如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB 上,点B,E在函数 ( )的图象上,若阴影部分的面积为12 - ,则点E的坐标是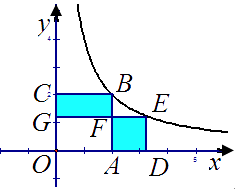
三、解答题
-
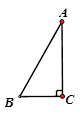
17. .18. 如图:在Rt△ABC中,∠C=90°,BC=8,∠B=60°, 求∠A的度数,AB和AC的值.
 19. 已知反比例函数 图象的两个分支分别位于第一、第三象限.(1)、求k的取值范围;
19. 已知反比例函数 图象的两个分支分别位于第一、第三象限.(1)、求k的取值范围;
(2)、取一个你认为符合条件的K值,写出反比例函数的表达式,并求出当x=﹣6时反比例函数y的值;
20. 已知圆内接正三角形边心距为2cm,求它的边长.
21. 已知:如图,D是BC上一点,△ABC∽△ADE,
求证:∠1=∠2=∠3 .
22. 如图,A,B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据: ≈1.732, ≈1.414)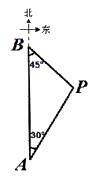 23. 如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.
23. 如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.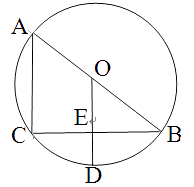 (1)、请写出两个不同的正确结论;(2)、若CB=8,ED=2,求⊙O的半径.
(1)、请写出两个不同的正确结论;(2)、若CB=8,ED=2,求⊙O的半径.
24. 密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.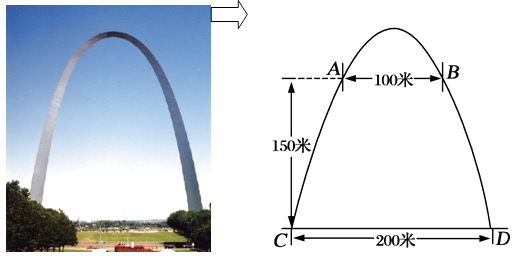 25. 如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB的延长线上的一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
25. 如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB的延长线上的一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.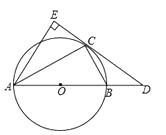
求证:DE是⊙O的切线.
26. 已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5). (1)、求抛物线的表达式及顶点坐标;
(1)、求抛物线的表达式及顶点坐标;
(2)、将抛物线沿x轴翻折,得到图象G,求图象G的表达式;(3)、在(2)的条件下,当-2<x<2时,直线y=m与该图象有一个公共点,求m的值或取值范围.
27. 如图,已知矩形 的边长 .某一时刻,动点 从 点出发沿 方向以 的速度向 点匀速运动;同时,动点 从 点出发沿 方向以 的速度向 点匀速运动,问: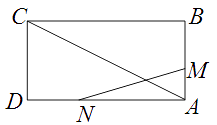 (1)、经过多少时间, 的面积等于矩形 面积的 ?
(1)、经过多少时间, 的面积等于矩形 面积的 ?
(2)、是否存在时刻t,使以A,M,N为顶点的三角形与 相似?若存在,求t的值;若不存在,请说明理由.
28. 综合题
(1)、探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.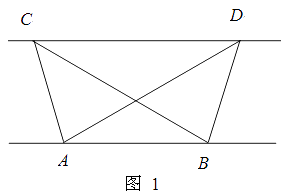 (2)、结论应用:① 如图2,点M,N在反比例函数 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
(2)、结论应用:① 如图2,点M,N在反比例函数 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行?请说明理由.
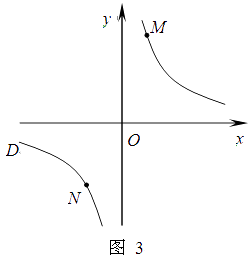 29. 设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数 ,当x=1时,y=3;当x=3时,y=1,即当 时,有 ,所以说函数 是闭区间[1,3]上的“闭函数”.(1)、反比例函数y= 是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;(2)、若二次函数y= 是闭区间[1,2]上的“闭函数”,求k的值;(3)、若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的表达式(用含m,n的代数式表示).
29. 设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数 ,当x=1时,y=3;当x=3时,y=1,即当 时,有 ,所以说函数 是闭区间[1,3]上的“闭函数”.(1)、反比例函数y= 是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;(2)、若二次函数y= 是闭区间[1,2]上的“闭函数”,求k的值;(3)、若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的表达式(用含m,n的代数式表示).