广东省揭阳市普侨等五校2015-2016学年八年级上册数学期末考试试卷

试卷更新日期：2018-01-15 类型：期末考试

进入出卷网下载

一、单选题

1. 在给出的一组数0，π， $\sqrt{5}$ ， 3.14， $\sqrt[3]{9}$ ， $\frac{22}{7}$ 中，无理数有（　　）

A、1个 B、2个 C、3个 D、5个

查看试题解析
2. $\sqrt{4}$ 的平方根是（）

A、4 B、2 C、 $\sqrt{2}$ D、± $\sqrt{2}$

查看试题解析
3. 如果 $\frac{1}{2}$ a^3xb^y与﹣a^2yb^x+1是同类项，则（）

A、 ${\begin{cases} x = - 2 \\ y = 3 \end{cases}$ B、 ${\begin{cases} x = 2 \\ y = - 3 \end{cases}$ C、 ${\begin{cases} x = - 2 \\ y = - 3 \end{cases}$ D、 ${\begin{cases} x = 2 \\ y = 3 \end{cases}$

查看试题解析
4. 在平面直角坐标系中，点 $P (- 20 ， a)$ 与点 $Q (b ， 13)$ 关于原点对称，则 $a + b$ 的值为（）

A、33 B、 $- 33$ C、 $- 7$ D、7

查看试题解析
5. P₁（x₁ ， y₁），P₂（x₂ ， y₂）是正比例函数 $y = - \frac{1}{2} x$ 图象上的两点，下列判断中，正确的是（）

A、y₁＞y₂ B、y₁＜y₂ C、当x₁＜x₂时，y₁＜y₂ D、当x₁＜x₂时，y₁＞y₂

查看试题解析
6. 下列条件中能得到平行线的是（）
①邻补角的角平分线；
②平行线内错角的角平分线；
③平行线同旁内角的角平分线．

A、①② B、②③ C、② D、③

查看试题解析
7. k、m、n为三个整数，若 $\sqrt{135}$ =k $\sqrt{15}$ ， $\sqrt{450}$ =15 $\sqrt{m}$ ， $\sqrt{180}$ =6 $\sqrt{n}$ ，则下列有关于k、m、n的大小关系，哪个正确？（）

A、k＜m=n B、m=n＜k C、m＜n＜k D、m＜k＜n

查看试题解析
8. 已知直线y=mx+n，其中m，n是常数且满足：m+n=6，mn=8，那么该直线经过（）

A、第二、三、四象限 B、第一、二、三象限 C、第一、三、四象限 D、第一、二、四象限

查看试题解析
9. 如图AB=AC，则数轴上点C所表示的数为（）

A、 $\sqrt{5}$ +1 B、 $\sqrt{5}$ －1 C、－ $\sqrt{5}$ +1 D、－ $\sqrt{5}$ －1

查看试题解析
10. 在直角坐标系中，已知A（1，1），在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P共有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若直角三角形两直角边的比是3：4，斜边长是20cm，则直角三角形的面积是．

查看试题解析
12. 已知 ${\begin{cases} x = 2 \\ y = 1 \end{cases}$ 是二元一次方程组 ${\begin{cases} m x + n y = 7 \\ n x - m y = 1 \end{cases}$ 的解，则m+3n的立方根为．

查看试题解析
13. 已知直线y=ax+b和直线y=kx交于点P（－4，－2），则关于x，y的二元一次方程组的解是．

查看试题解析
14. 过点P（8，2）且与直线y=x+1平行的一次函数解析式为．

查看试题解析
15. 在如图所示的平面直角坐标系中，点P是直线y=x上的动点，A（1，0），B（2，0）是x轴上的两点，则PA+PB的最小值为．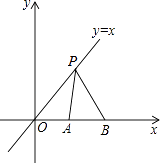

查看试题解析
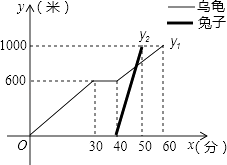
16. “龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场．图中的函数图象刻画了“龟兔再次赛跑”的故事（x表示乌龟从起点出发所行的时间，y₁表示乌龟所行的路程，y₂表示兔子所行的路程）．有下列说法：
①“龟兔再次赛跑”的路程为1000米；
②兔子和乌龟同时从起点出发；
③乌龟在途中休息了10分钟；
④兔子在途中750米处追上乌龟．
其中正确的说法是．（把你认为正确说法的序号都填上）

查看试题解析
17. 如图所示，折叠长方形ABCD的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm，求EF的长．

查看试题解析

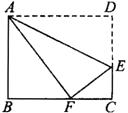
三、解答题

18. 解方程组： ${\begin{cases} 4x-3y = 11, （1） \\ 2x + y = 13 . （2） \end{cases}$

查看试题解析
19. 甲、乙两名同学进入初三后，某科6次考试成绩如图：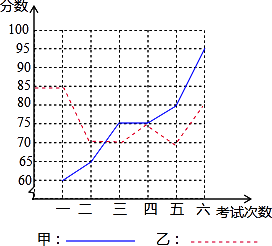

(1)、请根据下图填写如表：

平均数
方差
中位数
众数
极差
甲
75
75
乙
33.3
15

(2)、请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析：
①从平均数和方差相结合看；
②从折线图上两名同学分数的走势上看，你认为反映出什么问题？

查看试题解析
20. 已知△ABC的三边分别为m²－n² ， 2mn，m²+n²（m，n为正整数，且m＞n），
求证：△ABC是直角三角形

查看试题解析
21. 甲、乙两件服装的成本共500元，商店老板为获取利润，决定甲服装按50℅的利润标价，乙服装按40%的利润标价出售．在实际出售时，应顾客要求，两件服装均按标价的九折出售，这样商店共获利157元，求两件服装的成本各是多少元？

查看试题解析
22. 已知一次函数 $y = 3 x + m$ 和 $y = - x + n$ 的图象都经过点A $(- 2 ， 3)$ ，且与 $x$ 轴分别交于B，C两点，求△ ABC的面积．

查看试题解析
23. 综合题

(1)、如图，已知△ABC中，AD⊥BC于D， AE为∠BAC的平分线，∠B=50°，∠C=70°，求∠DAE的度数．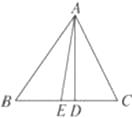

(2)、已知在△ABC中，AD⊥BC于点D，AE平分∠BAC（∠C>∠B）．求证：∠DAE= $\frac{1}{2}$ （∠C－∠B）．

查看试题解析
24. 一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两车在途中相遇后都停留一段时间，然后分别按原速一同驶往甲地后停车．设慢车行驶的时间为x小时，两车之间的距离为y千米，图中折线表示y与x之间的函数图象，请根据图象解决下列问题：

(1)、甲乙两地之间的距离为千米；

(2)、求快车和慢车的速度；

(3)、求线段DE所表示的y与x之间的函数关系式，并写出自变量x的取值范围.

查看试题解析
25. 某大酒店客房部有三人间、双人间和单人间客房，收费数据如下表（例如三人间普通间客房每人每天收费50元）．为吸引客源，在“十一黄金周”期间进行优惠大酬宾，凡团体入住一律五折优惠．一个50人的旅游团在十月二号到该酒店住宿，租住了一些三人间、双人间普通客房，并且每个客房正好住满，一天一共花去住宿费1510元．

普通间（元/人/天）
豪华间（元/人/天）
贵宾间（元/人/天）
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500

(1)、三人间、双人间普通客房各住了多少间？

(2)、设三人间共住了x人，则双人间住了人，一天一共花去住宿费用y元表示，写出y与x的函数关系式；

(3)、如果你作为旅游团团长，你认为上面这种住宿方式是不是费用最少？为什么？

查看试题解析

	普通间（元/人/天）	豪华间（元/人/天）	贵宾间（元/人/天）
三人间	50	100	500
双人间	70	150	800
单人间	100	200	1500

	平均数	方差	中位数	众数	极差
甲	75		75
乙		33.3			15