浙江省温州市瑞安市五校联考2017-2018学年九年级上册数学期末学业检测试卷
试卷更新日期:2018-01-15 类型:期末考试
一、选择题
-
1. 若 ,则 的值等于( )A、 B、 C、 D、2. 已知⊙O的半径为4cm,点P到圆心O的距离为3cm,则点P( )A、在圆内 B、在圆上 C、在圆外 D、不能确定3. 二次函数 的图象与y轴的交点坐标是( )
A、(0,1) B、(1,0) C、(-1,0) D、(0,-1)4. 若两个三角形的相似比为1:2,则它们的面积比为( )
A、1:2 B、1:4 C、2:1 D、4:15. 已知二次函数的图象(0≤ ≤4)如图,关于该函数在所给自变量的取值范围内,下列说法正确的是( ) A、有最大值2,有最小值-2.5 B、有最大值2,有最小值1.5 C、有最大值1.5,有最小值-2.5 D、有最大值1.5,有最小值36. 如图,D是外接圆 上的点,且∠CAD=20°,则∠ACD的度数为( )
A、有最大值2,有最小值-2.5 B、有最大值2,有最小值1.5 C、有最大值1.5,有最小值-2.5 D、有最大值1.5,有最小值36. 如图,D是外接圆 上的点,且∠CAD=20°,则∠ACD的度数为( ) A、20° B、30° C、40° D、45°7. 如图,有一块直角三角形余料ABC,∠BAC=90°,D是AC的中点,现从中切出一条矩形纸条DEFG,其中E,F在BC上,点G在AB上,若BF=4.5cm,CE=2cm,则纸条GD的长为( )
A、20° B、30° C、40° D、45°7. 如图,有一块直角三角形余料ABC,∠BAC=90°,D是AC的中点,现从中切出一条矩形纸条DEFG,其中E,F在BC上,点G在AB上,若BF=4.5cm,CE=2cm,则纸条GD的长为( )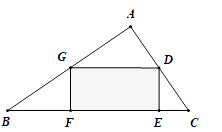 A、3 cm B、 cm C、 cm D、 cm8. 二次函数 与一次函数 的图象交于点A(2,5)和点B(3,m),要使 ,则 的取值范围是( )
A、3 cm B、 cm C、 cm D、 cm8. 二次函数 与一次函数 的图象交于点A(2,5)和点B(3,m),要使 ,则 的取值范围是( )
A、 B、 C、 D、 或9. 如图,点A,B,C均在坐标轴上,AO=BO=CO=1,过A,O,C作⊙D,E是⊙D上任意一点,连结CE, BE,则 的最大值是( )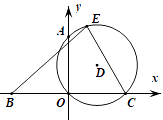 A、4 B、5 C、6 D、
A、4 B、5 C、6 D、二、填空题
-
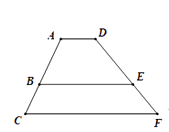
10. 某校九年1班共有 45位学生,其中男生有25人,现从中任选一位学生,选中女生的概率是11. 已知扇形的圆心角为120°,它的弧长为 ,则它的半径为 .12. 如图,点B,E分别在线段AC,DF上,若AD∥BE∥CF,AB=3,BC=2,DE=4.5,则DF的长为 .
 13. 若二次函数 的图象与x轴的一个交点是(2,0),则与x轴的另一个交点坐标是 .
13. 若二次函数 的图象与x轴的一个交点是(2,0),则与x轴的另一个交点坐标是 .
14. 如图,△ABC内接于⊙O,AD⊥BC于点D,AD=BD.若⊙O的半径OB=2,则AC的长为 .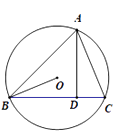 15. 两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了m,恰好把水喷到F处进行灭火.
15. 两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了m,恰好把水喷到F处进行灭火.
三、解答题
-
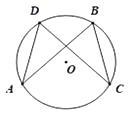
16. 如图,在⊙O中,AB=CD.求证:AD=BC.
 17. 一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有2个,若从中随机摸出一个球,这个球是白球的概率为 .
17. 一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有2个,若从中随机摸出一个球,这个球是白球的概率为 .
(1)、求袋子中白球的个数;(请通过列式或列方程解答)
(2)、随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
18. 如图,点O是线段AB的中点,根据要求完成下题: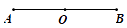 (1)、在图中补画完成:
(1)、在图中补画完成:第一步,以A B为直径的画出⊙O;
第二步,以B为圆心,以BO为半径画圆弧,交⊙O于点C,连接点CA,CO;
(2)、设AB=6,求扇形AOC的面积.(结果保留π)19. 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C'处,点D落在点D'处,C'D'交线段AE于点G.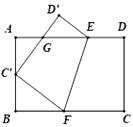 (1)、求证:△BC'F∽△AGC';(2)、若C'是AB的中点,AB=6,BC=9,求AG的长.20. 如图,二次函数的图象的顶点坐标为(1, ),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).
(1)、求证:△BC'F∽△AGC';(2)、若C'是AB的中点,AB=6,BC=9,求AG的长.20. 如图,二次函数的图象的顶点坐标为(1, ),现将等腰直角三角板直角顶点放在原点O,一个锐角顶点A在此二次函数的图象上,而另一个锐角顶点B在第二象限,且点A的坐标为(2,1).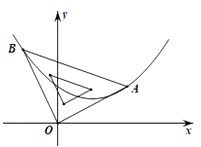 (1)、求该二次函数的表达式;(2)、判断点B是否在此二次函数的图象上,并说明理由.21. 甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)
(1)、求该二次函数的表达式;(2)、判断点B是否在此二次函数的图象上,并说明理由.21. 甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m) 22. 如图,二次函数 的图象与x轴交于点 A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
22. 如图,二次函数 的图象与x轴交于点 A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.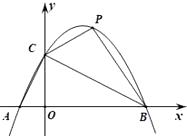 (1)、写出线段AC,BC的长度:AC= , BC=;(2)、记△BCP的面积为S,求S关于x的函数表达式;(3)、过点P作PH⊥BC,垂足为H,连结AH,AP,设AP与BC交于点K,探究:是否存在四边形ACPH为平行四边形?若存在,请求出 的值;若不存在,请说明理由,并求出 的最大值.23. 如图,AB是⊙O的直径, ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)、写出线段AC,BC的长度:AC= , BC=;(2)、记△BCP的面积为S,求S关于x的函数表达式;(3)、过点P作PH⊥BC,垂足为H,连结AH,AP,设AP与BC交于点K,探究:是否存在四边形ACPH为平行四边形?若存在,请求出 的值;若不存在,请说明理由,并求出 的最大值.23. 如图,AB是⊙O的直径, ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.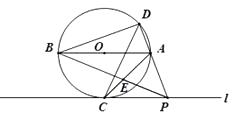 (1)、求∠BAC的度数;(2)、当点D在AB上方,且CD⊥BP时,求证:PC=AC;(3)、在点P的运动过程中
(1)、求∠BAC的度数;(2)、当点D在AB上方,且CD⊥BP时,求证:PC=AC;(3)、在点P的运动过程中①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD, DE,直接写出△BDE的面积.