四川省资阳市乐至县2016届九年级上学期数学期末考试试卷
试卷更新日期:2018-01-11 类型:期末考试
一、单选题
-
1. 下列二次根式中, 的同类根式是( )A、 B、 C、 D、2. 如图,在△ABC中,∠C=90°,AB=3,BC=2,则cosB的值是( )
 A、 B、 C、 D、3. 如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A、 B、 C、 D、3. 如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A、 B、
B、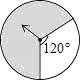 C、
C、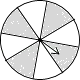 D、
D、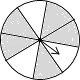 4. 判断一元二次方程x2﹣2x+1=0的根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根5. 如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
4. 判断一元二次方程x2﹣2x+1=0的根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根5. 如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( ) A、∠ABD=∠C B、∠ADB=∠ABC C、 D、6. 河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比是1: (坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A、∠ABD=∠C B、∠ADB=∠ABC C、 D、6. 河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比是1: (坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )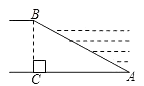 A、5 米 B、10米 C、15米 D、10 米7. 用配方法解方程x2﹣4x﹣3=0,下列配方结果正确的是( )A、(x﹣4)2=19 B、(x﹣2)2=7 C、(x+2)2=7 D、(x+4)2=198. 如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( )
A、5 米 B、10米 C、15米 D、10 米7. 用配方法解方程x2﹣4x﹣3=0,下列配方结果正确的是( )A、(x﹣4)2=19 B、(x﹣2)2=7 C、(x+2)2=7 D、(x+4)2=198. 如图,在平行四边形ABCD中,点E在CD上,若DE:CE=1:2,则△CEF与△ABF的周长比为( ) A、1:2 B、1:3 C、2:3 D、4:99. 某商品经过两次降价,零售价降为原来的 ,已知两次降价的百分率均为x,则列出方程正确的是( )
A、1:2 B、1:3 C、2:3 D、4:99. 某商品经过两次降价,零售价降为原来的 ,已知两次降价的百分率均为x,则列出方程正确的是( )
A、 B、 C、(1+x)2=2 D、(1﹣x)2=210. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△BDE∽△DPE;② = ;③DP2=PH•PB;④tan∠DBE=2﹣ .
其中正确的是( )
 A、①②③④ B、①②④ C、②③④ D、①③④
A、①②③④ B、①②④ C、②③④ D、①③④二、填空题
-
11. 当x时,二次根式 有意义.12. 已知: ,则 的值为 .13. 在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有3个红球且摸到红球的概率为 ,那么口袋中球的总个数为 .
14. 关于x的一元二次方程x2+2x+a=0的一个根为2,则它的另一个根为 .15. 如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,﹣1),则点B的坐标是 . 16. 如图,平行四边形ABCD中,∠B=30°,AB≠BC ,将△ABC沿AC翻折至△AB′C ,连结B ′D. 若 ,∠AB ′D=75°,则BC= .
16. 如图,平行四边形ABCD中,∠B=30°,AB≠BC ,将△ABC沿AC翻折至△AB′C ,连结B ′D. 若 ,∠AB ′D=75°,则BC= .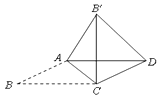
三、解答题
-
17. 计算(1)、(2)、 .18. 解方程
(1)、x2﹣4x﹣5=0(2)、2(x﹣2)2=(x﹣2)19. 为弘扬“东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.(1)、请直接写出第一位出场是女选手的概率;(2)、请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.20. 如图,某市对位于笔直公路上的两个小区A、B的供水路线进行优化改造,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区B到供水站M的距离为300米, (1)、求供水站M到公路AB的垂直距离MD的长度.(2)、求小区A到供水站M的距离.(结果可保留根号)21. 如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,连接DE,CF交AD于G,点E是BF中点.
(1)、求供水站M到公路AB的垂直距离MD的长度.(2)、求小区A到供水站M的距离.(结果可保留根号)21. 如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,连接DE,CF交AD于G,点E是BF中点. (1)、求证:△AFG∽△AED(2)、若FG=2,G为AD中点,求CG的长.22. 已知关于x的一元二次方程x2+2x+a﹣2=0.(1)、若该方程有两个不相等的实数根,求实数a的取值范围;
(1)、求证:△AFG∽△AED(2)、若FG=2,G为AD中点,求CG的长.22. 已知关于x的一元二次方程x2+2x+a﹣2=0.(1)、若该方程有两个不相等的实数根,求实数a的取值范围;
(2)、设方程两根为x1 , x2是否存在实数a,使 ?若存在求出实数a,若不存在,请说明理由.23. 小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米. (1)、若旗杆的高度FG是a米,用含a的代数式表示DG.(2)、小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上, ,结果精确到0.1)24. 如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
(1)、若旗杆的高度FG是a米,用含a的代数式表示DG.(2)、小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上, ,结果精确到0.1)24. 如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE. (1)、若a=5,sin∠ACB= ,求b.(2)、若a=5,b=10当BE⊥AC时,求出此时AE的长.(3)、设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
(1)、若a=5,sin∠ACB= ,求b.(2)、若a=5,b=10当BE⊥AC时,求出此时AE的长.(3)、设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.