四川省达州市2016届九年级上学期数学期末考试试卷
试卷更新日期:2018-01-11 类型:期末考试
一、单选题
-
1. 方程 x(x+3)= 0的根是( )A、x=0 B、x =-3 C、x1=0,x2=3 D、x1=0,x2=-32. 在双曲线 y=上有两点A ,B ,当 时,有 .则 的值可以是( )
A、2 B、1 C、0 D、、-13. 一个两位数,它的十位数字比个位数字大3,且十位数字与个位数字的积是28,求这个两位数.设这个两位数的个位数字为 ,则可列方程( )
A、 B、 C、 D、4. 以3,4为两边的三角形的第三边长是方程 的根,则这个三角形的周长为( )A、15或12 B、12 C、15 D、以上都不对5. 如图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,那么该几何体的主视图为( ) A、
A、 B、
B、 C、
C、 D、
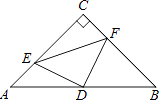
D、 6. 如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
6. 如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( ) A、 B、 C、4 D、87. 如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3 cm,那么AE等于( )
A、 B、 C、4 D、87. 如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3 cm,那么AE等于( ) A、3 cm B、 cm C、6 cm D、 cm8. 如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )
A、3 cm B、 cm C、6 cm D、 cm8. 如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )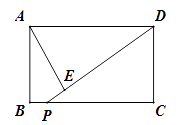 A、
A、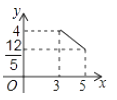 B、
B、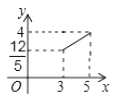 C、
C、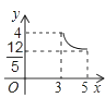 D、
D、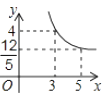 9. 李明同时掷甲、乙两枚质地均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).记甲立方体朝上一面上的数字为x、乙立方体朝上一面朝上的数字为y,这样就确定点P的一个坐标( , ),那么点P落在双曲线 上的概率为( )A、 B、 C、 D、10. 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
9. 李明同时掷甲、乙两枚质地均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).记甲立方体朝上一面上的数字为x、乙立方体朝上一面朝上的数字为y,这样就确定点P的一个坐标( , ),那么点P落在双曲线 上的概率为( )A、 B、 C、 D、10. 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 .
其中正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
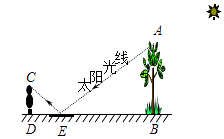
11. 已知函数 是反比例函数,则m的值为 .12. 如图,为了测量校园内一棵不可攀的树的高度,数学应用实践小组做了如下的探索实践:根据《物理学》中光的反射定律,利用一面镜子和一根皮尺,设计如图的测量方案:把镜子放在离树(AB)9米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.8米,则树(AB)的高度为米.
 13. 对于实数a,b,定义运算“*”: ,例如:4*2,因为4>2,所以4*2= -4×2=8.若 、 是一元二次方程 -5x+6=0的两个根,则 的值是 .
13. 对于实数a,b,定义运算“*”: ,例如:4*2,因为4>2,所以4*2= -4×2=8.若 、 是一元二次方程 -5x+6=0的两个根,则 的值是 .
14. 若关于 的一元二次方程 有两个不相等的实数根,则化简代数式 的结果是 .15. 设函数 与 的图象交点坐标为(a,b),则 的值为 .16. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6 ,AF=4 ,则AE的长为 .
三、解答题
-
17. 当x满足条件 时,求出方程x2﹣2x﹣4=0的根.
18. 如图,一次函数 的图像与反比例函数 ( 为常数,且 )的图像都经过点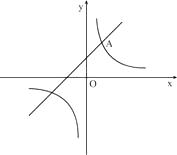 (1)、求点 的坐标及反比例函数的表达式;(2)、结合图像直接比较:当 时, 和 的大小.
(1)、求点 的坐标及反比例函数的表达式;(2)、结合图像直接比较:当 时, 和 的大小.
19. 某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4 860元的均价开盘销售.(1)、求平均每次下调的百分率.(2)、某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?20. 如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.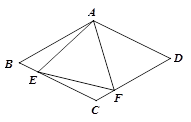 (1)、证明不论E、F在BC.CD上如何滑动,总有BE=CF;(2)、当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.21. 创建文明城市,人人参与,人人共建.我市各校积极参与创建活动,自发组织学生走上街头,开展文明劝导活动.某中学九(一)班为此次活动制作了大小、形状、质地等都相同的“文明劝导员”胸章和“文明监督岗”胸章若干,放入不透明的盒中,此时从盒中随机取出“文明劝导员”胸章的概率为
(1)、证明不论E、F在BC.CD上如何滑动,总有BE=CF;(2)、当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.21. 创建文明城市,人人参与,人人共建.我市各校积极参与创建活动,自发组织学生走上街头,开展文明劝导活动.某中学九(一)班为此次活动制作了大小、形状、质地等都相同的“文明劝导员”胸章和“文明监督岗”胸章若干,放入不透明的盒中,此时从盒中随机取出“文明劝导员”胸章的概率为 ;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为 . (1)、请你用所学知识计算:九(一)班制作的“文明劝导员”胸章和“文明监督岗”胸章各有多少只?(2)、若小明一次从盒内剩余胸章中任取2只,问恰有“文明劝导员”胸章、“文明监督岗”胸章各1只的概率是多少?(用列表法或树状图计算)
;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为 . (1)、请你用所学知识计算:九(一)班制作的“文明劝导员”胸章和“文明监督岗”胸章各有多少只?(2)、若小明一次从盒内剩余胸章中任取2只,问恰有“文明劝导员”胸章、“文明监督岗”胸章各1只的概率是多少?(用列表法或树状图计算)
22. 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8)、动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动、其中,点M沿OA向终点A运动,点N沿BC向终点C运动、过点N作NP⊥BC,交AC于P,连结MP、已知动点运动了t秒、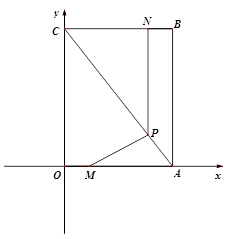 (1)、P点的坐标为( , )(用含t的代数式表示);(2)、试求 △MPA面积的最大值,并求此时t的值;(3)、请你探索:当t为何值时,△MPA是一个等腰三角形?23. 如图:抛物线y=- +bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC= ,tanα-tanβ=2,∠ACB=90°.
(1)、P点的坐标为( , )(用含t的代数式表示);(2)、试求 △MPA面积的最大值,并求此时t的值;(3)、请你探索:当t为何值时,△MPA是一个等腰三角形?23. 如图:抛物线y=- +bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC= ,tanα-tanβ=2,∠ACB=90°.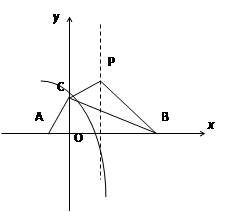 (1)、求点C的坐标;(2)、求抛物线的解析式;(3)、若抛物线的顶点为P,求四边形ABPC的面积.
(1)、求点C的坐标;(2)、求抛物线的解析式;(3)、若抛物线的顶点为P,求四边形ABPC的面积.