福建省仙游县第三教学片区2016届九年级上学期数学期末考试试卷B卷

试卷更新日期：2018-01-11 类型：期末考试

进入出卷网下载

一、单选题

1. 观察下列银行标志，从图案看既是轴对称图形又是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 在质地和颜色都相同的三张卡片的正面分别写有-2，-1，1，将三张卡片背面朝上洗匀，从中抽出一张，并记为x，然后从余下的两张中再抽出一张，记为y，则点（x，y）在反比例函数y= $\frac{2}{x}$ 图象上的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、1

查看试题解析
3. 某商品原价800元，连续两次降价a％后售价为578元，下列所列方程正确的是（）

A、800（1+a%）²=578 B、800（1－a%）²=578 C、800（1－2a%）=578 D、800（1－a²%）=578

查看试题解析
4. 一个密闭不透明的盒子里有若干个白球，在不允许将球倒出来数的情况下，为估计白球数，小刚向其中放入8个黑球摇匀后，从中随意摸出一个球记下颜色，再把它放回盒中，不断重复这一过程，共摸球100次，其中20次摸到黑球，你估计盒中大约有白球（）

A、20个 B、28个 C、36个 D、32个

查看试题解析
5. 如图，AB是⊙O的弦，AC是⊙O切线，A为切点，BC经过圆心．若∠B=20°，则∠C的大小等于（）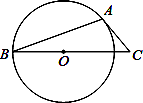

A、20° B、25° C、40° D、50°

查看试题解析
6. 如图，某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心，AB为半径的扇形(忽略铁丝的粗细)，则所得的扇形DAB的面积为（）

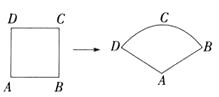A、6 B、7 C、8 D、9

查看试题解析
7. 将抛物线y=－2x²先向左平移1个单位，再向上平移3个单位，两次平移后得到的抛物线的解析式为（）

A、y=－2（x+1）²+3 B、y=－2（x+1）²-3 C、y=－2（x-1）²+3 D、y=－2（x-1）²-3

查看试题解析
8. 如图，Rt△ABC中，∠C=90°，AC=3，BC=4，若以A为旋转中心，将其按顺时针方向旋转60°到△AB'C'位置，则B点经过的路线长为（）

A、π B、 $\frac{4}{3}$ π C、 $\frac{5}{3}$ π D、 $\frac{5}{6} π$

查看试题解析
9. 如上图，经过原点O的⊙P与 $x$ 、 $y$ 轴分别交于A、B两点，点C是劣弧 $\overset{⌢}{O B}$ 上一点，则∠ACB=（）

A、80° B、90° C、100° D、无法确定

查看试题解析
10. 若两个扇形满足弧长的比等于它们半径的比，则称这两个扇形相似。如图，如果扇形AOB与扇形 $A_{1} 0_{1} B_{1}$ 是相似扇形，且半径 $O A ： O_{1} A_{1} = k$ ( $k$ 为不等于0的常数)。那么下面四个结论：①∠AOB＝∠ $A_{1} 0_{1} B_{1}$ ；②△AOB∽△ $A_{1} 0_{1} B_{1}$ ；③ $\frac{A B}{A_{1} B_{1}} = k$ ；④扇形AOB与扇形 $A_{1} 0_{1} B_{1}$ 的面积之比为 $k^{2}$ 。成立的个数为：（）

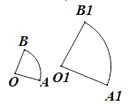A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若两个相似三角形的相似比是，则它们的面积比是．

查看试题解析
12. 已知直线 $l$ 与⊙O相切，若圆心O到直线 $l$ 的距离是5，则⊙O的半径是．

查看试题解析
13. 如图，已知A为⊙O外一点，连结OA交⊙O于P，AB为⊙O的切线，B为切点，AP＝5㎝，AB＝ $5 \sqrt{3}$ ㎝，则劣弧与AB，AP所围成的阴影的面积是.

查看试题解析
14. 抛物线 $y = - x^{2} + 2 x + m - 2$ 与y轴的交点为（0，－4）那么m＝．

查看试题解析
15. 一个y关于x的函数同时满足两个条件：①图象过(0，1)点；②当x＞0时，y随x的增大而减小．这个函数解析式为． (写出一个即可)

查看试题解析
16. 如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O₁ ， O₂ ， O₃ ， … 组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒 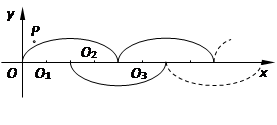$\frac{π}{2}$ 个单位长度，则第2016秒时，点P的坐标是

查看试题解析

三、解答题

17. 解方程：x（x-2）=3.

查看试题解析
18. 在平面直角坐标系中，的三个顶点坐标分别为A(2，-4)，B(3，-2)， C(6，-3).
①画出△ABC关于 $x$ 轴对称的△A₁B₁C₁；
②以M点为位似中心，在网格中画出△A₁B₁C₁的位似图形△A₂B₂C₂ ，使△A₂B₂C₂与△A₁B₁C₁的相似比为2︰1.

查看试题解析
19. 某工厂为了对新研发的一种产品进行合理定价，将该产品按拟定的价格进行试销，通过对5天的试销情况进行统计,得到如下数据：
单价x（元/件）
30
34
38
40
42
销量y（件）
40
32
24
20
16

(1)、通过对上面表格中的数据进行分析，发现销量 $y$ （件）与单价 $x$ （元/件）之间存在一次函数关系，求 $y$ 关于 $x$ 的函数关系式（不需要写出函数自变量的取值范围）；

(2)、预计在今后的销售中，销量与单价仍然存在（1）中的关系，且该产品的成本是20元/件.为使工厂获得最大利润，该产品的单价应定为多少?

查看试题解析
20. 如图所示，正比例函数 $y = \frac{1}{2} x$ 的图象与反比例函数 $y = \frac{k}{x}$ $(k \neq 0)$ 在第一象限的图象交于点 $A$ ，过点 $A$ 作 $x$ 轴的垂线，垂足为 $M$ ，已知△OAM的面积为1.

(1)、求反比例函数的解析式；

(2)、如果点 $B$ 为反比例函数在第一象限图象上的点（点 $B$ 与点 $A$ 不重合），且点 $B$ 的横坐标为1，在 $x$ 轴上求一点 $P$ ，使 $P A + P B$ 最小.

查看试题解析
21. 已知，如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．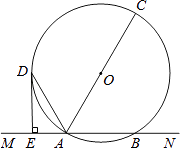

(1)、求证：DE是⊙O的切线；

(2)、若DE=6cm，AE=3cm，求⊙O的半径．

查看试题解析
22. 某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况，从九年级随机抽取部分女生进行该项目测试，并以测试数据为样本，绘制出如图所示的部分频数分布直方图（从左到右依次分为六个小组，每小组含最小值，不含最大值）和扇形统计图．根据统计图提供的信息解答下列问题：

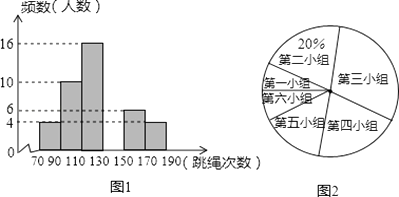(1)、补全频数分布直方图，并指出这个样本数据的中位数落在第小组；（1）

(2)、若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀，本校九年级女生共有260人，请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数；

(3)、如测试九年级女生“一分钟跳绳”次数不低于170次的成绩为满分，在这个样本中，从成绩为优秀的女生中任选一人，她的成绩为满分的概率是多少？

查看试题解析
23. 如图，已知 $A B$ 是 $⊙ O$ 的直径，过点 $O$ 作弦 $B C$ 的平行线，交过点 $A$ 的切线 $A P$ 于点 $P$ ，连结 $A C$ ．

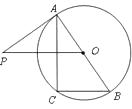(1)、求证： $△ A B C ∽ △ P O A$ ；

(2)、若 $O B = 2$ ， $O P = \frac{7}{2}$ ，求 $B C$ 的长．

查看试题解析
24. 类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整，原题：如图1，在平行四边形ABCD中，点E是BC的中点，点F是线段AE上一点，BF的延长线交射线CD于点G. 若 $\frac{A F}{E F} = 3$ ，求 $\frac{C D}{D G}$ 的值．

(1)、尝试探究：
在图1中，过点E作EH∥AB交BG于点H，则AB和EH的数量关系是，
CG和EH的数量关系是， $\frac{C D}{D G}$ 的值是．

(2)、类比延伸：如图2，在原题条件下，若 $\frac{A F}{E F} = m$ (m＞0)则 $\frac{C D}{D G}$ 的值是(用含有m的代数式表示)，试写出解答过程．

(3)、拓展迁移：如图3，梯形ABCD中，DC∥AB，点E是BC的延长线上的一点，AE和BD相交于点F，若 $\frac{A B}{C D} = a ， \frac{B C}{B E} = b$ (a＞0，b＞0)则 $\frac{A F}{E F}$ 的值是(用含a、b的代数式表示)．

查看试题解析
25. 如图，已知点A（3，0），以A为圆心作⊙A与Y轴切于原点，与x轴的另一个交点为B，过B作⊙A的切线l．

(1)、以直线l为对称轴的抛物线过点A及点C（0，9），求此抛物线的解析式；

(2)、抛物线与x轴的另一个交点为D，过D作⊙A的切线DE，E为切点，求DE的长；

(3)、点F是切线DE上的一个动点，当△BFD与△EAD相似时，求出BF的长．

查看试题解析

单价x（元/件）	30	34	38	40	42
销量y（件）	40	32	24	20	16