四川省泸州市泸县2015-2016学年八年级上学期数学期末考试试卷

试卷更新日期：2018-01-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列长度的三条线段能组成三角形的是（）

A、1，2，3 B、4，5，9 C、6，8，10 D、5，15，8

查看试题解析
2. 某种感冒病毒的直径为0.0000000031米，用科学记数法表示为（）

A、3.1×10^﹣9米 B、3.1×10⁹米 C、﹣3.1×10⁹米 D、0.31×10^﹣8米

查看试题解析
3. 下列计算正确的是（）

A、a•a²=a² B、（a²）²=a⁴ C、a²•a³=a⁶ D、（a²b）³=a²•a³

查看试题解析
4. 三角形的两个内角分别为60°和80°，则它的第三个内角的度数是（　　）

A、70° B、60° C、50° D、40°

查看试题解析
5. 下列分式是最简分式的是（）

A、 $\frac{2 x}{x^{2} + 1}$ B、 $\frac{x - 1}{x^{2} - 1}$ C、 $\frac{4}{2 x}$ D、 $\frac{1 - x}{x - 1}$

查看试题解析
6. 如图案是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 下列算式计算结果为x²﹣4x﹣12的是（）

A、（x+2）（x﹣6） B、（x﹣2）（x+6） C、（x+3）（x﹣4） D、（x﹣3）（x+4）

查看试题解析
8.
如图，在△ABC中，AB=AC，∠BAC=108°，点D在BC上，且BD=AB，连接AD，则∠CAD等于（　　）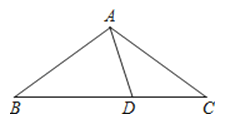

A、30° B、36° C、38° D、45°

查看试题解析
9. 下列各式中能用完全平方公式分解因式的是（）

A、x²+x+1 B、x²+2x+1 C、x²+2x﹣1 D、x²﹣2x﹣1

查看试题解析
10.
如图，在等腰直角△ABC中，∠ACB=90°，O是斜边AB的中点，点D、E分别在直角边AC、BC上，且∠DOE=90°，DE交OC于点P，则下列结论：①图中全等的三角形只有两对；②△ABC的面积等于四边形CDOE面积的2倍；③OD=OE；④CE+CD=BC，其中正确的结论有（　　）

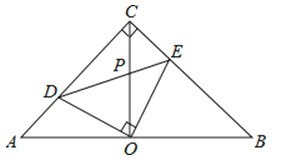A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则x的值等于．

查看试题解析
12. 六边形的内角和等于度．

查看试题解析
13. 在平面直角坐标系中，点P的坐标是（3，﹣2），则点P关于y轴对称的对称点的坐标是．

查看试题解析
14. 若等腰三角形的两条边长分别为7cm和14cm，则它的周长为 cm．

查看试题解析
15. 已知x^m=6，xⁿ=4，则x^m+n的值为．

查看试题解析
16. 分解因式：a⁴﹣16=.

查看试题解析
17. 已知 $\frac{1}{a} - \frac{1}{b} = \frac{1}{2}$ ，则 $\frac{a b}{a - b}$ 的值是．

查看试题解析
18.
如图，在△ABC中，AC=BC，△ABC的外角∠ACE=100°，则∠A= 度．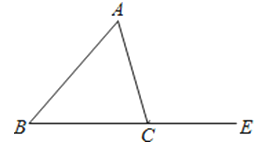

查看试题解析
19.
如图所示，已知点A、D、B、F在一条直线上，AC=EF，AD=FB，要使△ABC≌△FDE，还需添加一个条件，这个条件可以是　（只需填一个即可）

查看试题解析
20. 用正三角形、正四边形和正六边形按如图所示的规律拼图案，即从第二个图案开始，每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个，则第n个图案中正三角形的个数为（用含n的代数式表示）．

查看试题解析

三、解答题

21. 计算： $(1 - \frac{1}{x + 2}) \div \frac{x^{2} - 1}{x + 2}$ ．

查看试题解析
22. 因式分解：（x﹣y）³﹣4（x﹣y）．

查看试题解析
23. 如图，在△ABC中，∠C=90°，AB的垂直平分线DE交AC于D，垂足为E，若∠A=30°，CD=3．

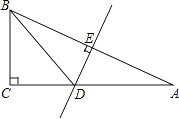(1)、求∠BDC的度数．

(2)、求AC的长度．

查看试题解析
24. 先化简，再求值：（a+2b）²+（a+b）（b﹣a），其中a=2，b=﹣1．

查看试题解析
25. 解方程： $\frac{x - 1}{x - 2} - 1 = \frac{8}{x^{2} - 4}$ ．

查看试题解析
26. 已知：如图，AB=AE，∠1=∠2，∠B=∠E．求证：BC=ED．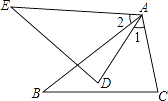

查看试题解析
27. △ABC在平面直角坐标系中的位置如图所示．A、B、C三点在格点上．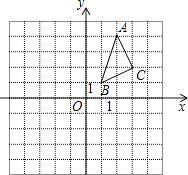

①作出△ABC关于x轴对称的△A₁B₁C₁ ，并写出点C₁的坐标；
②作出△ABC关于y对称的△A₂B₂C₂ ，并写出点C₂的坐标．

查看试题解析
28. 已知：如图，BE⊥CD于点E，BE=DE，BC=DA．判断DF与BC的位置关系，并说明理由．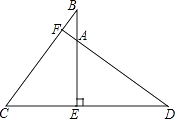

查看试题解析
29. 列方程解应用题
为了迎接春运高峰，铁路部门日前开始调整列车运行图，2015年春运将迎来“高铁时代”．甲、乙两个城市的火车站相距1280千米，加开高铁后，从甲站到乙站的运行时间缩短了11小时，大大方便了人们出行．已知高铁行使速度是原来火车速度的3.2倍，求高铁的行驶速度．

查看试题解析
30. 综合题探究发现

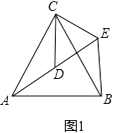
(1)、问题发现
如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
填空：①∠AEB的度数为；②线段AD，BE之间的数量关系为．

(2)、拓展探究
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．

查看试题解析